Faraday's law -- circular loop with a triangle

[TSny]

thats where i am having confusion how is it that in physics even in mechanics problems i can assume random direction but end up with a correct direction despite having used a wrong direction in calculations

Here's a long-winded attempt at an explanation. I'm sure others can do better.

Consider a resistor $R_1$ in a circuit. Suppose Bob chooses the direction of the unknown current $i_1$ through $R_1$ to be to the right while Jan chooses the direction to be to the left.

Suppose they are setting up $\sum \Delta V$ around a loop that contains $R_1$. We can also assume Bob and Jan go around the loop in the same direction and that this direction is such that they go from $a$ to $b$ when crossing $R_1$.

Then Bob would write the potential change from $a$ to $b$ as $\Delta V_{a \, \mapsto b} = -i_1 R_1$. Jan would write $\Delta V_{a \, \mapsto b} = +i_1 R_1$. It should be clear that wherever Bob has $i_1$ in an equation, Jan would have $-i_1$. (Same for a junction equation involving $i_1$.)

So, they will get the same answers for $i_1$ except they will get opposite signs. But note that they will both get the same magnitude and sign for the potential change $\Delta V_{a \, \mapsto b}$. The person who gets the positive answer for the current will have also have chosen the correct direction of the current.

For example, suppose that Bob gets a positive answer for $i_1$ when he solves the equations. Jan will necessarily get the negative of Bob’s answer. Based on their answers for $i_1$, both Bob and Jan will agree that the potential at $a$ is higher than the potential at $b$. But current flows from higher to lower potential. So Jan, who got the negative result for $i_1$, will conclude that she chose the wrong direction for the current. Bob, who got the positive answer for $i_1$, chose the correct direction.

 

[cnh1995]

@vishnu 73, your equations look correct to me. You can solve them simultaneously, get the six currents and find the line integral along path AB (and all other paths if you wish). That would be the " net emf" along side AB, which is not same when you choose different paths to go from A to B. What remains same is the "electrostatic potential difference" between A and B or V_AB.
Net emf is the resultant of electromagnetically induced emf and electrostatic potential difference.
So, for side AB, you know the net emf and electromagnetically induced emf. Find V_AB from that (take care of the polarity). I believe this is what the question in your OP is asking.

 

[timetraveller123]

@cnh1995 i am confused once again
1)what is net emf my guess is that if there was one and only equilateral triangle ABC then the net emf along AB is the k(area)/3 is that right
but in this case there is many more paths which have AB as one of their sides hence the sum of all such emf is the net emf along AB is that what net emf is
2)then no what is electrostatic potential difference prior to this problem my understanding is that electrostatic potential difference is just the difference in potential between two point
i am all confused with the terms again what is difference between net emf , electrostatic potential difference and how does that relate to V_ab

 

[timetraveller123]

@TSny
i am getting these are these correct
$I_1 = \frac{k(6A_1 - 1.5A_0 - 2A)}{12r_2}\\ I_3 = \frac{k(6A_1 + 1.5 A_o + 2A)}{-18r_2}$

 

[timetraveller123]

My thinking here was as follows: without the triangle we all agree the voltage between any 2 points along the circle = 0.

wait why is that so

 

[cnh1995]

I suspect the problem with the above is that the wire is also generating em

Exactly!

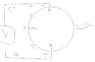
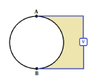
My thinking here was as follows: without the triangle we all agree the voltage between any 2 points along the circle = 0. So running a wire between those two points can't change voltages anywhere.

I agree with this part (voltage="electrostatic" voltage).

However, *instead of putting a triangle inside, if you just joined A and B, everything will change. ^#But if there is an equilateral triangle inscribed in the circle with all the sides having "equal" resistances, then again the electrostatic voltage will be zero.

Basically, KCL has to be satisfied at every node.
In the former case (*), in order to satisfy KCL at A and B, currents through the two parts of circumference would be unequal, because some of the current would flow through the wire joining A and B (Shape of this wire matters too.)
In the latter case(#), currents through all three sides of the equilateral triangle will be equal and currents through all three arcs of the circumference would also be equal and KCL will be satisfied at every node without developing any electrostatic voltage.

In OP's problem, the sides of the triangle have unequal resistances, hence, there is an electrostatic voltage present.

 

[cnh1995]

wait why is that so

See if this helps.
https://www.physicsforums.com/posts/5859178/
The page I've linked is from an excellent book. See if you can buy it if you want to learn circuits at a deeper, intuitive level.

 

[timetraveller123]

@cnh1995
sir thanks for the recomendations but right now it would be helpful if you could clear up just some doubts
so induced emf is like a non conservative battery
and
the potential difference between two points like in this question is the current in the branch * resistance of the branch
so in this question v_ab = I₁R₂
is these right
and you said when the resistances are the same in triangle there is potential diference between A and B is it because due to symetry
thanks for the help

 

[cnh1995]

the potential difference between two points like in this question is the current in the branch * resistance of the branch
so in this question vab = I1R2

No. I₁R₂ gives the "net" emf in branch AB.
This net emf has two components: one is electromagnetically induced emf and the other is electrostatic voltage developed because of surface charges. This electrostatic voltage is the potential difference between A and B. It is same for all the paths from A to B. Concept of potential can be applied only in electrostatic case.

 

[timetraveller123]

ok now it makes sense
just last doubt
in principle i could have gone through all the possible loops to calculate the net emf as well right?
and when you say electromagnetically induced emf it means kA_o/3 right?

 

[cnh1995]

in principle i could have gone through all the possible loops to calculate the net emf as well right?

Yes.

when you say electromagnetically induced emf it means kAo/3 right?

Yes, Ao is the area of the triangle.

 

[timetraveller123]

ok sir if i have this following circuit the

say the magnetic field is increasing into the page and the right resistor in r1 and left resistor is r2 there will be current in the clockwise direction induced after that how to solve the problem

 

[cnh1995]

ok sir if i have this following circuit the

I am 22 and I just graduated. No need to address me as 'sir'.

say the magnetic field is increasing into the page and the right resistor in r1

The current will be anticlockwise.
Let's take only one voltmeter and connect it first on the left and then on the right.
(Two voltmeters at the same time might make the problem complicated. I'll have to think about it.)
You can write KVL equation for the rectangular loop as follows: I(r1+r2)=AdB/dt.
This will give you the current I.

About the voltmeter reading:
If the voltmeter is placed on the left,
IR1+V_left=AdB/dt
So,
V_left=AdB/dt-IR₁

Similarly, if the voltmeter is placed on the right,
IR₂+V_right=AdB/dt

V_right=AdB/dt-IR₂.

Note that the polarities of the two voltmeter readings will be opposite. Can you say why?

 

[cnh1995]

Check out this video.
The exact same problem is discussed here by Prof Lewin.
.

 

[timetraveller123]

I am 22 and I just graduated. No need to address me as 'sir'.

no formalism but i am a indian i just address those who teach me as sir
actually i am coming from that video to here

Note that the polarities of the two voltmeter readings will be opposite. Can you say why?

wait why is it because of the different paths i have no clue
is this concept supposed to be hard or am i not getting it?

my question why can't the same reasoning be applied to a circuit with the magnetic field replaced with a battery i still can go in loops like this

 

[timetraveller123]

@rude man
what i am having trouble with is understanding all these terms and how they relate to each other
so if have the triangle without the circle all with same resistances then the emf induced in each of the legs will kA/3 the current through the triangle is kA/3r hence with this information how can i calculate the potential difference between two vertex

what does net emf mean ?
do i really have to know vector calculus to undestand all of this
thanks sir

 

[cnh1995]

do i really have to know vector calculus to undestand all of this

No, but having some intution about the line integral of E.dl will certainly help.

what does net emf mean ?

The line integral of E_net.dl, where E_net is the resultant of the induced electric field (non-conservative) and electrostatic field (conservative).

what i am having trouble with is understanding all these terms and how they relate to each other

Ok.
Maybe you should try a similar but simpler problem first.
The rate of change of flux through the following circular loop is 3V. Resistances of the green half and red half are 1 ohm and 2 ohm respectively.
What is the "potential difference" between A and B?

 

[cnh1995]

Assuming the voltmeter loop doesn't enclose any flux..

I told you the voltmeter reading between any two points along the circle without the triangle is zero. That was incorrect. If you hook up the voltmeter so that the leads and meter form a loop which does not encircle any B field, then the voltmeter reading would be iR where i = πa⋅dB/dt and R the resistance between the two points.

This would be true only if the circle does NOT have a uniform resistance, which is not the case with OP's circuit. The resistance of the circle in OP's diagram is uniform (3r₁) and hence, the voltmeter will read zero between any two points (without the triangle inscribed in the circle).

Edit: @rude man, I believe I have misinterpreted your setup. What you wrote is actually correct. See #72.

 

[cnh1995]

it is a triangle then wouldn't the magnitude of electric fields change along the triangle

Yes, but the integral of E.dl along the three sides will be the same, thanks to the symmetry of equilateral triangle. It is the line integral that you should be interested in, and not the actual electric field.

This is interesting! We have agreed that the line integral of E.dl along the three sides is same. It turns out that although the electric field at every point on the triangle is different in magnitude, its component "along" the side of the triangle is same at every point. You can see it by drawing concentric field lines. The electric field at some points is larger in magnitude, but its angle with the side is also bigger, so the components of the fields along the sides are equal at every point.

 

[timetraveller123]

This is interesting! We have agreed that the line integral of E.dl along the three sides is same. It turns out that although the electric field at every point on the triangle is different in magnitude, its component "along" the side of the triangle is same at every point. You can see it by drawing concentric field lines. The electric field at some points is larger in magnitude, but its angle with the side is also bigger, so the components of the fields along the sides are equal at every point.

yeah that part i got it when you related it to symetry

i was recently reading the other thread and you (@cnh1995) said given a circle with two halves of different resistances then the emf induced will be the same in both halves but due to different resistance the current due to induced emf will be different in the halves hence a electrostatic voltage is developed to even out the current in both the halves this made a whole lot of sense
is this so as to make the current in both halves the same?

now the question you gave me

emf induced along green loop = emf along red loop = 1.5 v
current through the loop = 1A
then how is the voltmeter connected ? doesn't the answer depend on that

 

[cnh1995]

is this so as to make the current in both halves the same?

Yes.

then how is the voltmeter connected ? doesn't the answer depend on that

There is no voltmeter. I asked for "potential difference", which means the electrostatic voltage between A and B. It is path independent.

Voltmeter reading will depend on how the meter is connected and you can work it out using the KVL equation for the voltmeter loop.

 

[timetraveller123]

ok then net emf along green is iR = 1v
induced emf = 1.5 v
so electrostatic voltage is -0.5v for green

for red it is 2-1.5 = 0.5v is this correct sir ?

 

[cnh1995]

so electrostatic voltage is -0.5v for green

for red it is 2-1.5 = 0.5v is this correct sir ?

It should be same for both the paths (or for all the paths joining A and B).

Assume the induced emf to be anticlockwise. What is the potential difference between A and B?

 

[timetraveller123]

okay is it

for red:
V_a -(i r₁ - ε/2) = v_b
for green :
V_a +(i r₂ - ε/2) = V_b
both gets -0.5v is that correct?

 

[cnh1995]

okay is it

for red:
V_a -(i r₁ - ε/2) = v_b
for green :
V_a +(i r₂ - ε/2) = V_b
both gets -0.5v is that correct?

Vb-Va=0.5V, means Vb is at 0.5V higher potential than Va. You can see the electrostatic voltage adds to the induced emf in 2 ohm and subtracts from the induced emf in 1 ohm.

 

[cnh1995]

If the voltmeter loop is to the left of the circle such that there is no B field anywhere inside the loop then the reading will be VB - VA = 1A x 1Ω = +1V, clockwise current assumed.

If the voltmeter loop is to the right of the circle such that there is no B field anywhere inside the loop then the reading will be VA - VB = 1A x 2Ω = +2V, clockwise current assumed.

Note the difference in polarity of the two voltages. B-A in one, A-B in the other.
@cnh1995 did I get that right?

Yes.

 

[timetraveller123]

wait so the potential between a and b is 0.5 v

@rude man
i thought we were using a anti clockwise current
so

how can i write the kvl for this voltmeter loop

 

[TSny]

@TSny
i am getting these are these correct
$I_1 = \frac{k(6A_1 - 1.5A_0 - 2A)}{12r_2}\\ I_3 = \frac{k(6A_1 + 1.5 A_o + 2A)}{-18r_2}$

Yes

 

[TSny]

If you hook up the voltmeter so that the leads and meter form a loop which does not encircle any B field, then the voltmeter reading would be iR where i = πa⋅dB/dt and R the resistance between the two points. Remember: the loop cannot encircle any B field. If the loop did include any B field you should expect the readings to be different and not just iR.

Assuming the voltmeter loop doesn't enclose any flux..

This would be true only if the circle does NOT have a uniform resistance, which is not the case with OP's circuit. The resistance of the circle in OP's diagram is uniform (3r₁) and hence, the voltmeter will read zero between any two points (without the triangle inscribed in the circle).

Is there a disagreement here? Let's make sure we are considering the same setup. We have a circular ring with B field confined to the interior of the ring.

I think the voltmeter would read iR as rude man says, where R is the resistance of the green section. This would be true whether or not the ring has a uniform resistance per unit length.

 

[timetraveller123]

The problem as stated in post 1 would generate a clockwise current. But in your post 49 you changed the sign of dB/dt so now with that change yes the current is counterclockwise.

oh @rude man i think we are talking about different questions i think i have my initial problem figured out now i am talking about the sample problem cnh 1995 gave me in post 55