ketanco
- 15
- 0
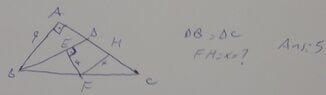
what is the length x? (FH and HC perpendicular too, which I missed to write)
I am totally stuck can not make any progress on this question. Answer should be 5. I don't know how to obtain it
View attachment 8571
I am totally stuck can not make any progress on this question. Answer should be 5. I don't know how to obtain it
View attachment 8571