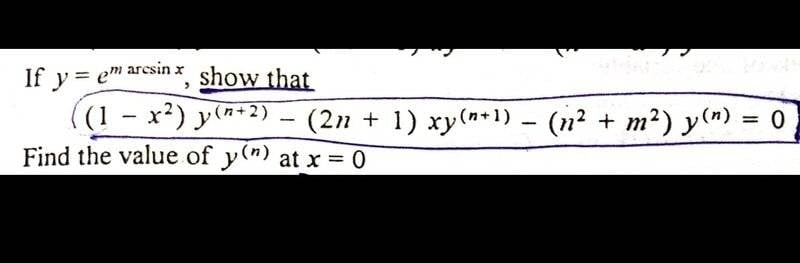Find nth derivative of e^m(arcsinx) where x=0

[Kumail Haider]

Homework Statement

Find nth derivative of e^m(arcsinx) where x=0

Relevant Equations

Leibnitz theorem
(f.b)n=fn.b +nfn-1.b1+.........+f.bn

Here is the problem that I'm trying to solve. I've done the first part that is prove but I'm. facing difficulty in finding nth derivative

I'm attaching pics of my attempt of solving this problem as I've no idea that how to type all these mathematical expressions.
Can anyone please guide me that how to find the nth derivative (it always confuses me )
I will be thankful for your guidance.

 

[BvU]

I've no idea how to type all these mathematical expressions.

The $\LaTeX$ Guide link is at the bottom left of the edit window !

But I grant you it's an awful lot of work... pure masochism to typeset all that stuff

So you start with
$$y^{(0)} = y = e^{m\arcsin x} \ \Rightarrow \ y^{(1)} = {m\over \sqrt{1-x^2}} \; e^{m\arcsin x} = {m\over \sqrt{1-x^2}} \; y$$and so $$
\begin {align*} y^{(2)} &= \left ( {m\over \sqrt{1-x^2}} \right )' \;y +{m\over \sqrt{1-x^2}} \; y' \\ \ \\
&={x\over 1-x^2} \left ( {m\over \sqrt{1-x^2}} \right ) \;y + {m^2\over 1-x^2} \;y \\ \ \\
&= {x\over 1-x^2}\; y^{(1)} + {m^2\over 1-x^2} \;y ^{(0)} \qquad\Rightarrow \\ \ \\
\left (1-x^2 \right )\; y^{(2)} &= x \; y^{(1)} + m^2\;y^{(0)} \tag 1
\end {align*}
$$Leibnitz proof is by induction, so with $(1)$ we have a statement $P_{n=0}$ :
$$\begin {align*} \left (1-x^2 \right )\; y^{(n+2)} &= (2n+1)\;x \; y^{(n+1)} + (n^2+m^2)\;y^{(n)} \tag 2\end {align*} $$ which is true for all $n$ if we can prove $P_{n}\Rightarrow P_{n+1}$.
To do that we differentiate $(2)$:
$$\begin {align*} -2x \; y^{(n+2)} + \left (1-x^2 \right ) \; y^{(n+3)} &= (2n+1) \; y^{(n+1)} + (2n+1)\;x \; y^{(n+2)} + (n^2+m^2)\;y^{(n+1)} \\ \ \\
\left (1-x^2 \right ) \; y^{(n+3)} &= (2n+3)\;x \; y^{(n+2)} + (n^2+ 2n+1+m^2)\;y^{(n+1)} \\ \ \\
\left (1-x^2 \right ) \; y^{(n+3)} &=\left (2(n+1)+1\right )\;x \; y^{(n+2)} + \left ( (n+1)^2+ m^2\right )\;y^{(n+1)}
\end {align*} $$which is $P_{n+1}$.

So there ! But you had already done that, witness the pictures :

I've done the first part that is prove

Now on to the ninth derivative, one way or the other.
Cheating isn't allowed, I suppose (anyway, the ninth derivative looks horrendous and I don't know if I can trust the result when my cheater substitutes $x=0$ )

And therefore, all I can come up with is brute force: use $(2)$ four times to ripple down from $y^{(9)}$ to $y^{(1)}$ which is $m$.

That is from $n=7$ in three steps of 2 to to $n=1$.

Fortunately, all $y^{(n+1)}$ have a factor $x$ in front, so they drop out at $x=0$.

That means: at $x=0$ we have $y^{(9)} |_{x=0}$ $= (7^2+m^2) \;y^{(7)} |_{x=0}$ and so on.

So brute force yields $$y^{(9)} |_{x=0} = (49+m^2)(25+m^2)(9+m^2)(1+m^2)m$$And I am way too lazy to work this out myself. But it turns out the cheater is pretty consistent with $m(m^8 + 84 m^6 + 1974 m^4 + 12916 m^2 + 11025)$ as before. Hurray!

And as a farewell present, usable for the umpteenth derivative as well:$$y^{(2n+1)} |_{x=0} = m\;\prod_{k=1}^n \left( (2k-1)^2+m^2\right ) $$I think ...

[edit] And it's pure fun to do $y^{(2n)} |_{x=0}$ and find (almost) the same expression ! Am I overdoing...?

(but now I have robbed you of your exercise... violating PF rules. Sorry about that, but I couldn't resist )

Let me pick up at your

$A$ is correct, but $B$ seems to be in error. I leave it to you to find the minus sign in your picture ....



$\$

 

[vela]

Can anyone please guide me that how to find the nth derivative (it always confuses me )

It looks like you have the basic idea. Just keep writing terms and look for the pattern (if it isn't apparent from what you've done already).

 

[vela]

Now on to the ninth derivative, one way or the other.

nth ≠ ninth :)

 

[Kumail Haider]

Let me pick up at your

View attachment 325221$A$ is correct, but $B$ seems to be in error. I leave it to you to find the minus sign in your picture ....



$\$

Thanks a lot for your guidance

So, B = −(1−m^2) (m)

In that(which I've done)
I write equation $B$ down as :
−(1−m^2) = (m^2−1)
It means that I've multipled the whole bracket with this negative sign. Am I picking the right point?

 

[BvU]

nth ≠ ninth :)

How on earth did that 9 creep into my brain !
That means that $y^{(2n)} |_{x=0}$ comes into the picture too. Good thing I had fun deriving $$
y^{(2n)} |_{x=0} =\prod_{k=0}^n \left( (2k-1)^2+m^2\right )$$so almost the same expression -- but I am at a loss trying to merge the two into a single one..... help !

Probably B = −(1−m^2 )(m)
Am I write know?

I think it's going wrong here already:

That should be a minus sign, which turns your 3 into my $(2)$ and then it agrees with

 

[Kumail Haider]

View attachment 325240

That should be a minus sign, which turns your 3 into my $(2)$ and then it agrees with
That should be a minus sign, which turns your 3 into my $(2)$ and then it agrees with

View attachment 325242

Thanks
I think I get the point. I was making mistake in taking derivative of √(1−x ²) it should be −2x /2√(1−x ²)

Is this the mistake that I was making?

 

[BvU]

Indeed...