Jaccobtw
- 163
- 32
- Homework Statement
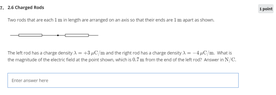
- Two rods that are each 1m in length are arranged on an axis so that their ends are 1m apart as shown. The left rod has a charge density λ=+3μC/m and the right rod has a charge density λ=−4μC/m. What is the magnitude of the electric field at the point shown, which is 0.7m from the end of the left rod? Answer in N/C.
- Relevant Equations
- dE = (kλdx)/(x+a)^2
λ1 = 3 microC/m λ2= -4 microC/m
__________ . __________
l----L1---l-a1-l-a2-l-----L2---l
(Not to scale)
L1 = length of rod 1 (1m)
a1 = length of end of rod 1 to point (0.7m)
L2 = length of rod 2 (1m)
a2 = length of end of rod 2 to point (0.3m)
k = e field constant (9.0e9)
Integrate both sides of dE = (kλdx)/(x+a)^2 from 0 to L
Eventually you get (kλ)(1/a - 1/(a+L))
Because the electric field is positive from the left rod and negative from the right rod, we know the electric field will point to the right at the point so we can add the electric fields together.
((λ1k)(1/a1 - 1/(a1+L1)) + ((λ2k)(1/a2 - 1/(a2+L2))Plug in numbers and add together:
114997 N/C
__________ . __________
l----L1---l-a1-l-a2-l-----L2---l
(Not to scale)
L1 = length of rod 1 (1m)
a1 = length of end of rod 1 to point (0.7m)
L2 = length of rod 2 (1m)
a2 = length of end of rod 2 to point (0.3m)
k = e field constant (9.0e9)
Integrate both sides of dE = (kλdx)/(x+a)^2 from 0 to L
Eventually you get (kλ)(1/a - 1/(a+L))
Because the electric field is positive from the left rod and negative from the right rod, we know the electric field will point to the right at the point so we can add the electric fields together.
((λ1k)(1/a1 - 1/(a1+L1)) + ((λ2k)(1/a2 - 1/(a2+L2))Plug in numbers and add together:
114997 N/C