Engineering Find the flux due to a vector crossing an open surface

Click For Summary
The discussion centers on calculating the flux of a vector field across an open surface. The user presents their vector field A as rz~hat(θ) and computes the curl, arriving at the result (z/r)~hat(k) - hat(r). They seek confirmation of their calculation, questioning discrepancies with provided answers. The conversation highlights the importance of ensuring consistent field definitions in vector calculus problems. Accurate verification of vector operations is crucial for understanding flux in open surfaces.
falyusuf
Messages
35
Reaction score
3
Homework Statement
Attached below.
Relevant Equations
Attached below.
Question:
1646434170915.png

Equations:
1646434303623.png

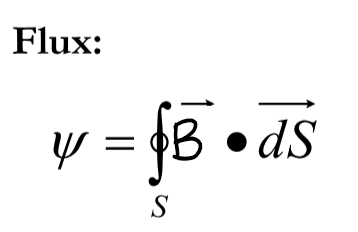
My attempt:
1646434736987.png


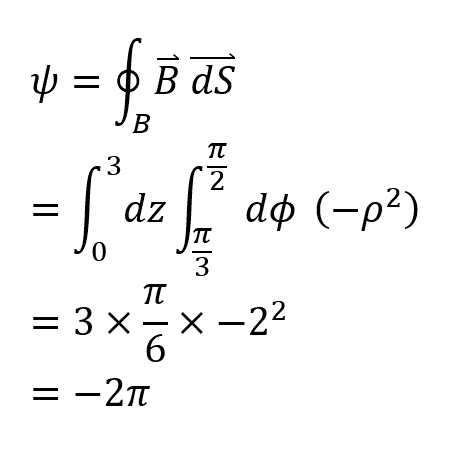
Could someone confirm my answer please?
 
Physics news on Phys.org
If ## \bf A = rz~ \hat {\bf \theta} ##
then ## \nabla \times \bf A = (z/r)~ \hat {\bf k} - \hat {\bf r} ##
and not what is given.
Different fields ??
 
Thread 'Why wasn’t gravity included in the potential energy for this problem?'

Thread 'Why wasn’t gravity included in the potential energy for this problem?'

I’m looking at the attached vibration problem. The solution in the manual includes the spring potential energy but does NOT include the gravitational potential energy of the hanging mass. Can someone explain why gravitational potential energy is not included when deriving the equation of motion? I tried asking ChatGPT but kept going in circles and couldn't figure out. Thanks!
View full post »

Similar threads

Engineering Calculating the flux through the spherical surfaces at certain radius
  • · Replies 13 ·
Replies
13
Views
2K
Engineering Calculating maximum flux density
  • · Replies 6 ·
Replies
6
Views
2K
Flux through a cylindrical surface enclosing part of a sphere
  • · Replies 9 ·
Replies
9
Views
801
Engineering Calculating the flux through a certain radius (concentric charged spheres)
  • · Replies 5 ·
Replies
5
Views
2K
Engineering Tubular Reactor with catalytic walls
  • · Replies 6 ·
Replies
6
Views
2K
Flux of constant magnetic field through lateral surface of cylinder
  • · Replies 7 ·
Replies
7
Views
2K
Engineering Find the electric field intensity due to a point, line, and plane
  • · Replies 3 ·
Replies
3
Views
2K
Engineering Resultant magnetic flux in a 3-phase induction motor
  • · Replies 16 ·
Replies
16
Views
7K
Find surface of maximum flux given the vector field's potential
  • · Replies 6 ·
Replies
6
Views
2K
Engineering Calculating Q such that E(0,0,0)=0
  • · Replies 2 ·
Replies
2
Views
974