hello478
- 165
- 14
- Homework Statement
- At time t = 0 waves are in phase. At dotted line, t = 18 s.
At which time is phase difference between the two oscillations ⅛ of a cycle?
A 4.0 s B 4.5 s C 8.0 s D 9.0 s
- Relevant Equations
- answer is B
attempt:
4 waves in first wave
4.5 waves in second wave
0.5 is the difference
and so they are in anti-phase at 18 secs
180º = phase difference for 18 secs
so then after that i cant figure a way to solve it out...
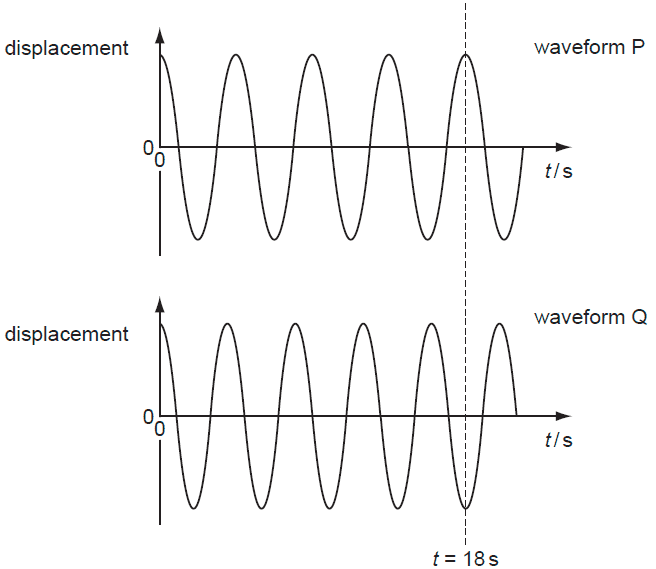
4 waves in first wave
4.5 waves in second wave
0.5 is the difference
and so they are in anti-phase at 18 secs
180º = phase difference for 18 secs
so then after that i cant figure a way to solve it out...
