Find the radius of the smaller circle in the tangent problem

[chwala]

Homework Statement

see attached

Relevant Equations

pythagoras theorem

Find the question here and the solution i.e number 10 indicated as $6-4\sqrt{2}$,

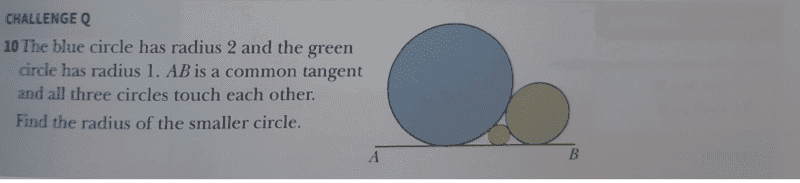
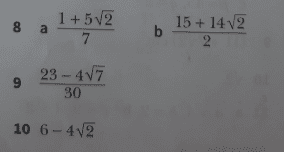
I am getting a different solution, my approach is as follows. I made use of pythagoras theorem for the three right angle triangles as follows,
Let radius of the smaller circle be equal to $c$ and distance from mid point of smaller circle to circle with radius $1=x$ then it follows that,
$x^2+(1-c)^2=(1+c)^2$
$x^2=4c$

let us also have the distance from the smaller circle to circle with radius $2=y$, then it follows that,
$y^2+(2-c)^2=(2+c)^2$
$y^2=8c$

Let $y^2+x^2=AB$, then it follows that, $(AB)^2 + (2-1)^2=3^2$
$AB=2\sqrt{2}$
then it follows that, $\sqrt{8}=2\sqrt{c}+2\sqrt{2c}$

Am i missing something here!

i got it!
$\sqrt{c}$=$\dfrac {\sqrt {8}}{2+2\sqrt{2}}$
⇒$c=0.34314575$ Bingo guys! Phew i took time on this men!

 

[anuttarasammyak]

Another approach by introducing Cartesian coordinates.
Equation of circle blue
$$x^2+y^2=2^2$$
Equation of circle green
$$(x-3)^2+y^2=1^2$$
Equation of common tangent line
$$y=\frac{1}{2\sqrt{2}}(x-6)$$
Let equation of circle red be
$$x^2+y^2+2px+2qy=r$$
which is tangential to all these three figures. Thus we can have three linear equations of p, q and r, and get
$$c=\sqrt{r+p^2+q^2}$$

More simply from the figure
$$2\tan^{-1}\frac{c}{4}=tan^{-1}\frac{1}{2\sqrt{2}}$$
$$c= 4 \tan (\frac{1}{2}tan^{-1}\frac{1}{2\sqrt{2}})=4\tan (\frac{sin \theta}{1+cos \theta})$$
where $\theta=tan^{-1}\frac{1}{2\sqrt{2}}$
$$c=4\tan \frac{1/3}{1+2\sqrt{2}/3}=4\tan (3-2\sqrt{2})\approx 0.012$$
I should appreciate if you would check whether it works or not.

 

[chwala]

Another approach by introducing Cartesian coordinates.
Equation of circle blue
$$x^2+y^2=2^2$$
Equation of circle green
$$(x-3)^2+y^2=1^2$$
Equation of common tangent line
$$y=\frac{1}{2\sqrt{2}}(x-6)$$
Let equation of circle red be
$$x^2+y^2+2px+2qy=r$$
which is tangential to all these three figures. Thus we can have three linear equations of p, q and r, and get
$$c=\sqrt{r+p^2+q^2}$$

More simply from the figure
$$2\tan^{-1}\frac{c}{4}=tan^{-1}\frac{1}{2\sqrt{2}}$$
$$c= 4 \tan (\frac{1}{2}tan^{-1}\frac{1}{2\sqrt{2}})=4\tan (\frac{sin \theta}{1+cos \theta})$$
where $\theta=tan^{-1}\frac{1}{2\sqrt{2}}$
$$c=4\tan \frac{1/3}{1+2\sqrt{2}/3}=4\tan (3-2\sqrt{2})\approx 0.012$$
I should appreciate if you would check whether it works or not.

$$c=4\tan \frac{1/3}{1+2\sqrt{2}/3}=4\tan (3-2\sqrt{2})\approx 0.012$$


I am afraid this does not look correct, i overlooked your solution. I have just checked it in detail...

 

[anuttarasammyak]

I made a mistake. Thanks for your effort.

 

[chwala]

I was thinking of using linear scale factor...i do not know whether that's possible. i'll try check it out...

 

[anuttarasammyak]

Let me try again. Observing angles which the triangle whose vertexes are center of circles and horizontal line on which center of orange circle lies make,
$$\alpha+\beta+\gamma=\pi$$
where
$$\sin\alpha=\frac{2-c}{2+c}$$
$$\sin\gamma=\frac{1-c}{1+c}$$
$$3^2=(2+c)^2+(1+c)^2-2 (2+c)(1+c)\cos\beta$$
This leads to $c=6-4\sqrt{2}$ which is same as OP.