chwala
Gold Member
- 2,827
- 415
- Homework Statement
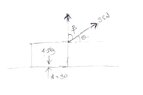
- A block of wood of mass ##4.5## kg rests on a table. A force of magnitude ##35## N, acting upwards at an angle ##θ^0## to the horizontal, is applied to the block but does not move it. Given that the normal contact force between the block and the tablke has magnitude ##30## N. Calculate
a. the value of ##θ##.
b. the frictional force acting on the block.
- Relevant Equations
- Mechanics
Refreshing on this...This is a relatively new area to me ...my solutions should be correct...what i am trying to engage on is if there are any other ways of looking at the same problem.
Ok in my working i have,
##30 + 35 \cos β-45=0##
##\cos β=0.4286##
##β = 64.62^0, ⇒θ=25.4^0 ## to one decimal place.
for part b,
##35\cos 25.4^0 -F=0##
##F=31.6 N##
any insight is welcome...
Ok in my working i have,
##30 + 35 \cos β-45=0##
##\cos β=0.4286##
##β = 64.62^0, ⇒θ=25.4^0 ## to one decimal place.
for part b,
##35\cos 25.4^0 -F=0##
##F=31.6 N##
any insight is welcome...
Attachments
Last edited: