- #1
Find the value of the trigonometric sum
- Thread starter Amlan mihir
- Start date
In summary, the conversation is about solving a math problem that involves using trigonometric identities and the unit circle. The hints provided suggest using different angles and applying trigonometric formulas to simplify the problem. The final solution involves taking the sum of cosines of specific angles and using symmetry to simplify the equation. The final result is that the sum of cosines is equal to -1/2.
- #2
BvU
Science Advisor
Homework Helper
- 16,104
- 4,865
Must be the hint that throws you off. What can it be aiming at ? Pick some angle ##\alpha## and multiply with ##\sin\alpha## to see what you get.
You know that ##sin(n\pi)=0## so maybe there's something.
Or else perhaps make a cosine sketch marking the given angles ?
You know that ##sin(n\pi)=0## so maybe there's something.
Or else perhaps make a cosine sketch marking the given angles ?
- #3
- 8,943
- 2,949
Here's another hint: Pick some number ##\alpha##, multiply ##S## by ##sin(\alpha)##, and then use the fact that ##sin(\alpha)cos(\beta) = \frac{1}{2} (sin(\alpha + \beta) + sin(\alpha - \beta))##. If you pick ##\alpha## cleverly, you get some amazing cancellations to get a very simple result.
Last edited:
- #4
Amlan mihir
- 3
- 2
solved it! , taking α as π/7 and using product to sum conversion for trig identities , it boils down to -[1][/2]
- #5
ehild
Homework Helper
- 15,542
- 1,917
Congratulation that you solved the problem. Here is an other way:
See the unit circle with 7 symmetrical vectors, with angle θ=2pi/7 between them. Their sum is zero, and so is the sum of the x components:cos(0) + cos(θ) +cos(2θ)+cos(3θ)+cos(4θ)+cos(5θ) +cos (6θ)=0. Because of symmetry, cos(θ)=cos (6θ) , cos(2θ)=cos(5θ) and cos(3θ)=cos(4θ). Therefore, 2(cos(θ) +cos(2θ)+cos(3θ))+1=0, cos(θ) +cos(2θ)+cos(3θ)=-1/2
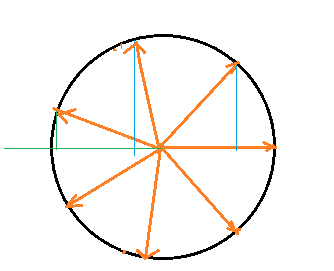
See the unit circle with 7 symmetrical vectors, with angle θ=2pi/7 between them. Their sum is zero, and so is the sum of the x components:cos(0) + cos(θ) +cos(2θ)+cos(3θ)+cos(4θ)+cos(5θ) +cos (6θ)=0. Because of symmetry, cos(θ)=cos (6θ) , cos(2θ)=cos(5θ) and cos(3θ)=cos(4θ). Therefore, 2(cos(θ) +cos(2θ)+cos(3θ))+1=0, cos(θ) +cos(2θ)+cos(3θ)=-1/2
Attachments
Last edited:
FAQ: Find the value of the trigonometric sum
1. What is a trigonometric sum?
A trigonometric sum is an equation that involves adding or subtracting trigonometric functions, such as sine, cosine, and tangent.
2. How do you find the value of a trigonometric sum?
To find the value of a trigonometric sum, you must use trigonometric identities and properties to simplify the equation and then use a calculator or reference table to evaluate the remaining values.
3. What are some common trigonometric identities used to simplify a sum?
Some common trigonometric identities include the Pythagorean identities, double angle identities, and sum and difference identities.
4. Can you provide an example of finding the value of a trigonometric sum?
Sure, let's say we have the equation sin(x) + cos(x). Using the sum identity, we can rewrite this as √2(sin(x+π/4)). From there, we can use a calculator to evaluate the sine of the angle (x+π/4) and then multiply by √2 to get the final value.
5. Are there any tips for solving trigonometric sums more efficiently?
One tip is to always check if there are any common factors or terms that can be factored out before applying identities. Additionally, knowing and memorizing common identities can help simplify equations faster.