- #1
chwala
Gold Member
- 2,825
- 413
- Homework Statement
- See attached
- Relevant Equations
- Understanding of vectors
Find the question and its solution below;
Ok i realized that we could also use cosine rule here, in my approach i considered the sketch below;
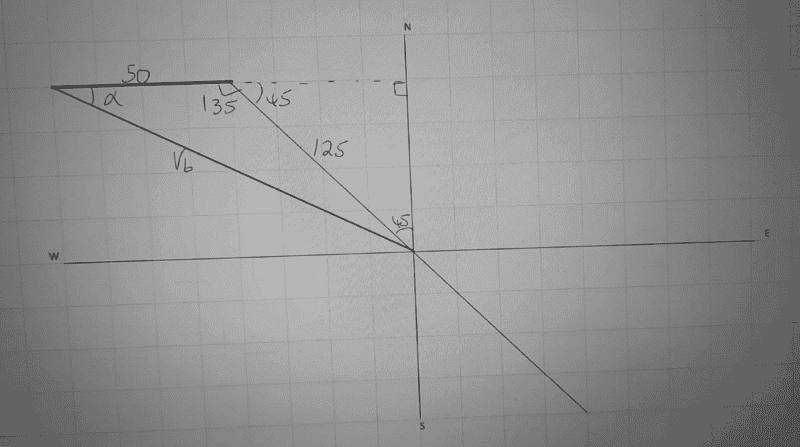
##V_b= 18,125- (2×50×125×cos 135)##
##V_b=164.2##
To find direction, i used sine rule;
##\frac {125}{sin α}##=##\frac {164.2}{sin 135}##
##α=32.56##
Would this be correct? ...i can see there is a small difference on the value of the magnitude.
##V_b= 18,125- (2×50×125×cos 135)##
##V_b=164.2##
To find direction, i used sine rule;
##\frac {125}{sin α}##=##\frac {164.2}{sin 135}##
##α=32.56##
Would this be correct? ...i can see there is a small difference on the value of the magnitude.
