JaySean
- 15
- 0
1. Not sure if it's the right forum but I'll try. The velocity of an particle varies quadratic with a formula based on time
a) Find the equation for acceleration and length as a function of time.
b) a = 3 m/s^3 (I think it's alpha)
Find the acceleration when t1=2s t2=5s and how big is the mean acceleration in the time intervall t2-t1.
2. See picture3. a) I think you can use the formula
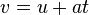 saying u=0 (start velocity) and say a=(v-u)/t
saying u=0 (start velocity) and say a=(v-u)/t
And do the same for
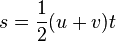 where s= length. But is it that easy or are they looking for a different solution, as this is something I learned few years ago. Or do I have to antiderivate it, which would make it complicated because there is no known fact.
where s= length. But is it that easy or are they looking for a different solution, as this is something I learned few years ago. Or do I have to antiderivate it, which would make it complicated because there is no known fact.
b) If a) is right could I then say solve v(t) which gives me t=3 alpha= 3 --> v(t)=27 m/s, and then get acceleration by the 2nd formula
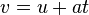 v= 27 u=0 t=3, so acceleration is 9? Or am I on the wrong way?
v= 27 u=0 t=3, so acceleration is 9? Or am I on the wrong way?
a) Find the equation for acceleration and length as a function of time.
b) a = 3 m/s^3 (I think it's alpha)
Find the acceleration when t1=2s t2=5s and how big is the mean acceleration in the time intervall t2-t1.
2. See picture3. a) I think you can use the formula
And do the same for
b) If a) is right could I then say solve v(t) which gives me t=3 alpha= 3 --> v(t)=27 m/s, and then get acceleration by the 2nd formula