anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
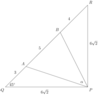
Let $PQR$ be a triangle with $\angle P=90^{\circ}$ and $PQ=PR$. Let $A$ and $B$ be points on the segment $QR$ such that $QA:AB:BR=3:5:4$. Find $\angle APB$.