Goomba
- 10
- 0
I am given the following circuit:
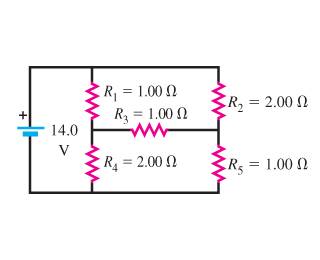
How do I find the current through the battery? I have trouble seeing which resistors are in series and which resistors are in parallel. I think I need to figure that out and then calculate R_eq accordingly. Then set I=V/R and solve for I.
But which resistors are in series and which are in parallel? It's confusing the way the circuit is laid out here...
How do I find the current through the battery? I have trouble seeing which resistors are in series and which resistors are in parallel. I think I need to figure that out and then calculate R_eq accordingly. Then set I=V/R and solve for I.
But which resistors are in series and which are in parallel? It's confusing the way the circuit is laid out here...