MHB Finding the final distance for the compressing in a spring system

[cbarker1]

Dear Every one,

Here is the question to the problem:

As shown in the figure below, a box of mass m = 5.00 kg is sliding across a horizontal frictionless surface with an initial speed v_i = 2.40 m/s when it encounters a spring of constant k = 2230 N/m. The box comes momentarily to rest after compressing the spring some amount x_c. Determine the final compression x_c of the spring.

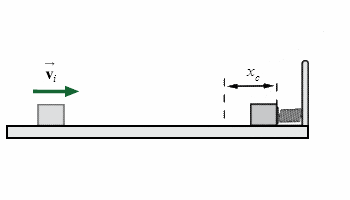
Is there way to use the Work-Energy Thereom to solve this problem? If so, you help me through step by step directions?
Thanks,
Cbarker1

 

[skeeter]

kinetic energy of the mass = potential energy stored in the spring

graph of kinetic energy and elastic potential energy vs position ...

 

[MarkFL]

Let's look at this dynamically, where time $t=0$ coincides with the time the box first contacts the spring, and orient our $x$-axis of motion such that the origin coincides with the point where the box first contacts the spring. Using Newton's 2nd law of motion, and Hooke's law we obtain the IVP:

$$mx''(t)=-kx(t)$$ where $$x'(0)=v_i,\,x(0)=0$$

Let's write the ODE in standard linear form:

$$x''(t)+\frac{k}{m}x(t)=0$$

By the theory of 2nd order linear homogeneous ODE's, we know the solution will take the form:

$$x(t)=c_1\cos\left(\sqrt{\frac{k}{m}}t\right)+c_2\sin\left(\sqrt{\frac{k}{m}}t\right)$$

Hence:

$$x'(t)=-c_1\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)+c_2\sqrt{\frac{k}{m}}\cos\left(\sqrt{\frac{k}{m}}t\right)$$

Using the given initial conditions, we obtain the system:

$$0=c_1$$

$$v_i=c_2\sqrt{\frac{k}{m}}\implies c_2=\sqrt{\frac{m}{k}}v_i$$

And so the solution to the IVP is given by:

$$x(t)=\sqrt{\frac{m}{k}}v_i\sin\left(\sqrt{\frac{k}{m}}t\right)$$ where $$0\le t\le\sqrt{\frac{m}{k}}\pi$$

And we have:

$$x'(t)=v_i\cos\left(\sqrt{\frac{k}{m}}t\right)$$

When the spring reaches maximal compression, we must have:

$$x'(t)=0\implies \sqrt{\frac{k}{m}}t=\frac{\pi}{2}\implies t=\sqrt{\frac{m}{k}}\cdot\frac{\pi}{2}$$

And so we find:

$$x_c=x\left(\sqrt{\frac{m}{k}}\cdot\frac{\pi}{2}\right)=\sqrt{\frac{m}{k}}v_i\sin\left(\sqrt{\frac{k}{m}}\cdot\sqrt{\frac{m}{k}}\cdot\frac{\pi}{2}\right)=\sqrt{\frac{m}{k}}v_i$$

Now, if we use energy considerations, we know the initial kinetic energy of the box must equal the work done to compress the spring when the spring reaches maximal compression:

$$\frac{1}{2}mv_i^2=\frac{1}{2}kx_c^2$$

Solving for $x_c$, we find:

$$x_c=\sqrt{\frac{m}{k}}v_i\quad\checkmark$$

Notice this formula is not only dimensionally consistent, but it also makes sense when we look at what happens when we change any of the parameters:

• Increase/decrease the mass of the box, and the compression distance increases/decreases too.
• Increase/decrease the stiffness of the spring and the compression distance decreases/increases.
• Increase/decrease the initial velocity of the box, and the compression distance increases/decreases too.