jbriggs444
Science Advisor
Homework Helper
2024 Award
- 13,345
- 8,024
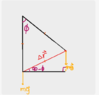
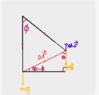
You cannot model an object which bends at the waist as a point-like object. Nor can a point-like object pump up the amplitude of its swing. It will just swing back and forth in an arc with a fixed amplitude. It has no degrees of freedom to influence anything.Callumnc1 said:Thank you for your reply @Lnewqban !
I don't think so since spider man can be modelled as a particle in circular motion when he bends his waist (assuming COM at waistline).
With an extended body, one can pump a rope or swing in either of two modes.
Mode 1: You utilize the angular momentum of your body to shift the ropes or chains fore and aft as you swing. You shift aft during the forward swing and fore during the aft swing. This works for low amplitudes, though it is rather difficult to get started. From a seated posture, the main things you are doing is leaning back with legs extended forward and pulling back on the chain or leaning forward with legs folded beneath the seat and pushing forward on the chain. From a standing posture, the main thing you are doing is leaning forward and pushing forward on the chain or leaning back and pulling back.
Mode 2: You shift your body up and down. Suddenly up at the bottom of the stroke. Slowly down anywhere near the end points. The more work you feel like you are doing, the more energy you are pumping into the system. This works exceptionally well at high amplitudes and is best done from a standing posture.
As a child, I had a chance to practice extensively since we had a longer-than-usual swing on one of the elm trees in our back yard. Maybe 15 feet of chain. It had a flat wooden seat and could be pumped from either a standing or a seated posture. From a standing posture, it was possible to get the chains a bit above the horizontal. I do not know how our parents failed to have heart attacks watching us every day.