HornetHades
- 2
- 0
1. Homework Statement

g = (Gm)/r2
I tried doing (Gm1)/a2 = (Gm2)/(r-a)2 where a is equal to the distance from the position we're trying to find to the center of the most massive object but end up getting a quadratic in the denominator on the right side. The answer in the back of the textbook is this:
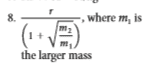
Thank you!
Homework Equations
g = (Gm)/r2
The Attempt at a Solution
I tried doing (Gm1)/a2 = (Gm2)/(r-a)2 where a is equal to the distance from the position we're trying to find to the center of the most massive object but end up getting a quadratic in the denominator on the right side. The answer in the back of the textbook is this:
Thank you!