Engineering First order circuit with DC sources

[Blehs]

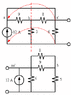
The circuit is in the attachment, plus the values that I've managed to find out so far.

Im having problem with figuring out the voltage at t=infinity.

So far i know that when t->infinity that inductors become short circuit. It says to apply current division and then Ohm's Law as a hint, and that's where I am stuffing up.

What i would like to know is - when the switch is closed, does current NOT flow through any of the resistors afterwards? Cause when i try to trace current flow, it ends up flowing through all the resistors anyway.

I tried doing current division; 9//5 = 3.214 ohms
then 3.214 + 8 = 11.214
then 12 x [ 11.214/(6+11.214) ] to determine current through the 6 ohm resistor

multiplying that by 6 gives me 46.904 A

the answer is 43.644 A

 

[gneill]

Current will flow through the resistors. And yes, a long time after t=0 the inductor becomes an effective short circuit.

Note that the 9 and 5 ohm resistors are not in parallel. However, when the switch is closed, note that the 9 and 8 Ohm resistors are connected at each end -- so they become parallel connected! That also places the 6 Ohm resistor in parallel with the 12A supply current. So imagine "folding" the circuit along the 5 Ohm--Inductor line. If you redraw the circuit accordingly, it should considerably simplify its appearance. See the attached figure.

The resistor network is then amenable to simplification down to a single resistance.

 

[Blehs]

Ok so BEFORE the circuit is redrawn, and there's just a single wire with no resistor on it connecting a and a' - if you were to trace the current from the 12A source wouldn't the current simply bypass the 9 ohm resistor and go through the short circuit all the way to a'? Then the current would split in two to go through the 8 and 6 ohm resistors.

In the redrawn circuit, it shows that the current actually splits 3-ways into the 8, 9 and 6 ohm resistors.

 

[gneill]

Ok so BEFORE the circuit is redrawn, and there's just a single wire with no resistor on it connecting a and a' - if you were to trace the current from the 12A source wouldn't the current simply bypass the 9 ohm resistor and go through the short circuit all the way to a'? Then the current would split in two to go through the 8 and 6 ohm resistors.

Why would it bypass a perfectly good path to where it wants to go (back to the bottom terminal of the current source)? The current will split into as many paths as are made available to it, dividing according to the relative conductances,

In the redrawn circuit, it shows that the current actually splits 3-ways into the 8, 9 and 6 ohm resistors.

Yup. As it does in the pre-redrawn circuit!

 

[Blehs]

I learned that when current reaches a crossroads, then the current likes to choose the path with less resistance. Since the wire is practically at zero resistance then wouldn't all current flow through the short circuit instead?

 

[gneill]

I learned that when current reaches a crossroads, then the current likes to choose the path with less resistance. Since the wire is practically at zero resistance then wouldn't all current flow through the short circuit instead?

That is not quite correct.

The current divides according to the relative conductances of the paths (conductance being the inverse of resistance). By "path" we mean the entire path back to the source or to where all the paths to choose from join up again, not just to the next node in line for an individual path!

Some current flows through all paths unless one of the paths happens to be zero resistance (infinite conductance!) and bypasses all of the other paths to the current's final destination.

In the attached figure, i2 and i3 will be nonzero; Not all of the current flows through the lowest value of resistance!

 

[Blehs]

That is not quite correct.

The current divides according to the relative conductances of the paths (conductance being the inverse of resistance). By "path" we mean the entire path back to the source or to where all the paths to choose from join up again, not just to the next node in line for an individual path!

Some current flows through all paths unless one of the paths happens to be zero resistance (infinite conductance!) and bypasses all of the other paths to the current's final destination.

In the attached figure, i2 and i3 will be nonzero; Not all of the current flows through the lowest value of resistance!

WOW that clears up so much. Alright i get it now =] Thnx heaps for the help, will be useful for my upcoming exam in 2 days time =P