alexlsu
- 1
- 0
- TL;DR
- How much flow rate is needed to either keep an object suspended in a large ID pipe section or to lift the object into the next section?
I have an object being forced up a vertical pipe with a slightly larger ID than the object by water. Then, the object reaches an area with a much larger ID than an object. How much flow fluid do I need to keep the object moving through the larger ID section and reach back into a small ID section? This is simplified for calculation. There are tapered areas to help guide the object into the next section. I need to know if the object will stall in the larger ID section due to fluid bypassing around it.
Smaller ID: 1.049 inches (0.027 m)
Larger ID: 1.800 inches (0.046 m)
Length of section: 24 inches (0.610 m)
Object OD: 0.955 inches (0.024 m)
Object Weight: 3 lbs (13.34 Newtons)
Use standard water as fluid: 1.0 SG
Flow rate available: up to 43 GPM (0.00276 m3/s)
Pressure is not an issue.
I tried using force calculations of the moving water against the object, and the results didn't look correct. For example, the object is 3 lbs (13.3 Newtons), and the water flow force in the large section (ID=1.8") at 43 GPM is 2.32 Newtons. So, at the max flow rate, the fluid would not be able to lift the object. Even as the fluid is moving at 1.7 m/s.
We know from practice that the object will move with no issues in the 1.049" ID pipe as the clearance between the ID and OD is very small.
Any help is appreciated.
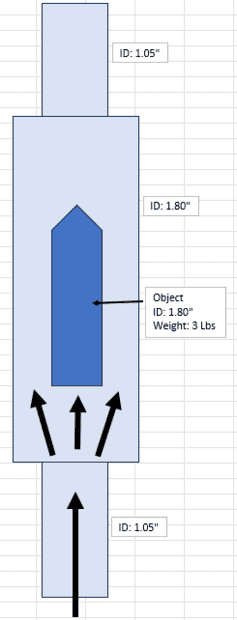
Smaller ID: 1.049 inches (0.027 m)
Larger ID: 1.800 inches (0.046 m)
Length of section: 24 inches (0.610 m)
Object OD: 0.955 inches (0.024 m)
Object Weight: 3 lbs (13.34 Newtons)
Use standard water as fluid: 1.0 SG
Flow rate available: up to 43 GPM (0.00276 m3/s)
Pressure is not an issue.
I tried using force calculations of the moving water against the object, and the results didn't look correct. For example, the object is 3 lbs (13.3 Newtons), and the water flow force in the large section (ID=1.8") at 43 GPM is 2.32 Newtons. So, at the max flow rate, the fluid would not be able to lift the object. Even as the fluid is moving at 1.7 m/s.
We know from practice that the object will move with no issues in the 1.049" ID pipe as the clearance between the ID and OD is very small.
Any help is appreciated.