For which case would the applied force be greater?

[paulimerci]

Homework Statement

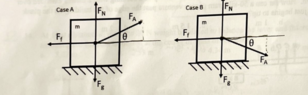
Assuming constant velocity, for which case would the applied force be greater?

Relevant Equations

F = ma

If F is applied at an angle above the horizontal, it decreases the normal force and vice versa.
So in case A,
net force along X = F applied cos theta - friction
since the object is moving with constant velocity, a = 0 and so the above equation becomes
F applied cos theta = friction
Now along the y axis,
net force along Y = N + F applied sin theta - mg
Since the object is not moving vertically F net in the y direction is taken zero,
0 = N + F applied sin theta - mg
N = mg - F applied sin theta

Similarly for case B,
N = mg + F applied sin theta
From the equations above for normal force we can say that F applied is greater for case B than case A. Is my solution right?

 

[Lnewqban]

 

[kuruman]

Your conclusion does not follow from the premises. I am not saying it's incorrect, it just doesn't follow. I suggest that in each of the two cases you derive an expression for F_applied and draw your conclusion based on a comparison between the two expressions. You have all the pieces, so just put them together.

 

[berkeman]

From the equations above for normal force we can say that F applied is greater for case B than case A. Is my solution right?

You have the right idea in mind and right answer, but as @kuruman says above, you have not completed the logical argument to justify your conclusion (so close though!).

So the final part that is missing is to talk about how the angle of the pulling force decreases or increases the normal force of the mass on the friction plane, and how that changes N and the retarding friction force for each scenario. Can you post a final answer with all of that included?

 

[haruspex]

In case you are not seeing why objections are being made, go through the algebra again being very careful only to use the same variable for forces that are necessarily the same.

 

[paulimerci]

You have the right idea in mind and right answer, but as @kuruman says above, you have not completed the logical argument to justify your conclusion (so close though!).

So the final part that is missing is to talk about how the angle of the pulling force decreases or increases the normal force of the mass on the friction plane, and how that changes N and the retarding friction force for each scenario. Can you post a final answer with all of that included?

For case A,
F applied = mg - N/ sin theta
For case B,
F applied = N-mg/ sin theta
To conclude: For case A, Applied force is maximum when the angle of the pulling force is minimum. Thereby when the applied force is greater, N will be smaller. Similarly for case B, the applied force is maximum only when the angle of the pulling force is minimum, in here as applied force increase N also increases. Therefore I can conclude saying case B's applied force is greater than case A.

 

[haruspex]

For case A,
F applied = mg - N/ sin theta
For case B,
F applied = N-mg/ sin theta
To conclude: For case A, Applied force is maximum when the angle of the pulling force is minimum. Thereby when the applied force is greater, N will be smaller. Similarly for case B, the applied force is maximum only when the angle of the pulling force is minimum, in here as applied force increase N also increases. Therefore I can conclude saying case B's applied force is greater than case A.

You are still using N for two different forces.

 

[paulimerci]

You are still using N for two different forces.

I'm I missing something? I don't get it!

 

[Lnewqban]

I'm I missing something? I don't get it!

The magnitude of N changes for each case due to the direction of the vertical component of the applied force.
Making a free body diagram of each case can clarify that.

 

[haruspex]

I'm I missing something? I don't get it!

In post #1 you wrote:

"N = mg - F applied sin theta​

Similarly for case B,​

N = mg + F applied sin theta"​

You have no reason to assume N is the same in both cases, and you know F won't be. So write $N_A=mg-F_A$, $N_B=mg+F_B$.
Whoops, I meant of course $N_A=mg-F_A\sin(\theta)$, $N_B=mg+F_B\sin(\theta)$

 

[paulimerci]

In post #1 you wrote:

"N = mg - F applied sin theta​

Similarly for case B,​

N = mg + F applied sin theta"​

You have no reason to assume N is the same in both cases, and you know F won't be. So write $N_A=mg-F_A$, $N_B=mg+F_B$.

Yes, I should have done that.

 

[paulimerci]

The magnitude of N changes for each case due to the direction of the vertical component of the applied force.
Making a free body diagram of each case can clarify that.

I understand N is smaller in case A and larger in case B. How do these change in angles one above horizontal (case A) and below horizontal (case B) decide for N? I'm confused on that part. Can you explain how?

 

[PeroK]

I understand N is smaller in case A and larger in case B.

I understand that $N_A < N_B$. Or, I understand the normal force is smaller ...

 

[Lnewqban]

I understand N is smaller in case A and larger in case B. How do these change in angles one above horizontal (case A) and below horizontal (case B) decide for N? I'm confused on that part. Can you explain how?

The normal-to-the-surface force can be a unique force, or a summation of forces.
That is where a FBD helps by showing all those forces and their directions.

Please, see:
https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/6-2-friction/

 

[paulimerci]

I understand that $N_A < N_B$. Or, I understand the normal force is smaller ...

I understand as $N_A < N_B$.

 

[haruspex]

Yes, I should have done that.

ok, so use that form (as corrected now in post #10). Use the same notation for the horizontal force balance equations, then combine them to eliminate $N_A, N_B$.

 

[paulimerci]

ok, so use that form (as corrected now in post #10). Use the same notation for the horizontal force balance equations, then combine them to eliminate $N_A, N_B$.

If $N_A, N_B$ are two different forces, is it possible to eliminate them? so do you want me to substitute $F_A=F_F$ and ##F_B=F_F# for horizontal component to the applied force in the vertical component? The frictional force are different in both cases right?

 

[haruspex]

If $N_A, N_B$ are two different forces, is it possible to eliminate them?

Yes.
In post #1 you wrote "F applied cos theta = friction". Rewrite that as $F_A \cos(\theta) = F_{friction,A}$, as I advised in post #16.
What equation relates $N_A, F_{friction,A}$?

 

[paulimerci]

Yes.
In post #1 you wrote "F applied cos theta = friction". Rewrite that as $F_A \cos(\theta) = F_{friction,A}$, as I advised in post #16.
What equation relates $N_A, F_{friction,A}$?

$F_{friction,A}=μ N_A$
$F_{friction,B}=μ N_B$
substituting the above equations in horizontal equations we get,
$F_A \cos(\theta)=μ N_A$
$F_B \cos(\theta)=μ N_B$
substituting the above equations in equations for vertical we get,
$F_A = μ mg/ \cos(\theta)+μ$
$F_B = μ mg/ \cos(\theta)-μ$

 

[haruspex]

$F_A=μ N_A$

No, $F_{friction,A}=μ N_A$

 

[paulimerci]

No, $F_{friction,A}=μ N_A$

Have I done it right?

 

[haruspex]

substituting the above equations in horizontal equations we get,
$F_A \cos(\theta)=μ N_A$
$F_B \cos(\theta)=μ N_B$
substituting the above equations in equations for vertical we get,
$F_A = μ mg/ \cos(\theta)+μ$
$F_B = μ mg/ \cos(\theta)-μ$

I assume you mean $F_A = μ mg/ (\cos(\theta)+μ)$, but that's not right either. What happened to sin(theta)?

 

[paulimerci]

I assume you mean $F_A = μ mg/ (\cos(\theta)+μ)$, but that's not right either. What happened to sin(theta)?

yeah, I forgot to include that!

 

[haruspex]

yeah, I forgot to include that!

so what do you get now?

 

[paulimerci]

so what do you get now?

I got
$F_A = μ mg/ {cos\theta}+μ {sin\theta}$
$F_B = μ mg/ {cos\theta}-μ {sin\theta}$

 

[haruspex]

I got
$F_A = μ mg/ {cos\theta}+μ {sin\theta}$
$F_B = μ mg/ {cos\theta}-μ {sin\theta}$

Please use parentheses appropriately. What you posted says $F_A = (μ mg/ {\cos(\theta}))+μ {\sin(\theta)}$, which is nonsense. I hope you mean $F_A = μ mg/ ({\cos(\theta})+μ {\sin(\theta}))$.
Having obtained the equations which give $F_A$ and $F_B$ in terms of m, g, μ and θ, you are now in a position to answer the question in post #1.

Btw, if you put a \ in front of cos, sin etc. in the LaTeX it will stop those functions being shown in italics. This helps to distinguish them from variables.

 

[paulimerci]

Please use parentheses appropriately. What you posted says $F_A = (μ mg/ {\cos(\theta}))+μ {\sin(\theta)}$, which is nonsense. I hope you mean $F_A = μ mg/ ({\cos(\theta})+μ {\sin(\theta}))$.
Having obtained the equations which give $F_A$ and $F_B$ in terms of m, g, μ and θ, you are now in a position to answer the question in post #1.

Btw, if you put a \ in front of cos, sin etc. in the LaTeX it will stop those functions being shown in italics. This helps to distinguish them from variables.

It's quite confusing when I use LaTeX I miss them when I type.
Now these equations gives a clear picture of the problem stated. Looks like I get it. I typed in real numbers to find solution and I found $F_B > F_A$

 

[haruspex]

It's quite confusing when I use LaTeX I miss them when I type.

You can use the magnifying glass icon at the right-hand end of the tools bar to preview your post. It's a toggle. Sometimes you need to refresh the window for it to work.

I typed in real numbers to find solution

That does not constitute a mathematical proof. You should be able to look at those two equations and see a reason that $F_B>F_A$ provided $\mu>0$ and $\theta>0$

 

[paulimerci]

You can use the magnifying glass icon at the right-hand end of the tools bar to preview your post. It's a toggle. Sometimes you need to refresh the window for it to work.

That does not constitute a mathematical proof. You should be able to look at those two equations and see a reason that $F_B>F_A$ provided $\mu>0$ and $\theta>0$

how should I do that? Can you give an example?

 

[PeroK]

I got
$F_A = μ mg/ {cos\theta}+μ {sin\theta}$
$F_B = μ mg/ {cos\theta}-μ {sin\theta}$

It's better to use the Latex "\frac" and perhaps double dollar delimiters:
$$F_A = \frac{\mu mg}{\cos\theta +\mu \sin\theta}$$$$F_B = \frac{\mu mg}{\cos\theta -\mu \sin\theta}$$If you reply to this post you'll see the Latex I used.

 

[haruspex]

how should I do that? Can you give an example?

Assuming x>y>0, which is larger, $x-y$ or $x+y$?
What about $\frac 1{x-y}$ and $\frac 1{x+y}$?

 

[paulimerci]

Assuming x>y>0, which is larger, $x-y$ or $x+y$?
What about $\frac 1{x-y}$ and $\frac 1{x+y}$?

X+y and 1/(x+y) are greater.
Thank you all for your great help!

 

[haruspex]

X+y and 1/(x+y) are greater.

3>2, so is 1/3 >1/2 or 1/2>1/3?

 

[paulimerci]

1/2>1/3

 

[haruspex]

1/2>1/3

Right, so if $x+y>x-y$ is $\frac 1{x+y}>\frac1{x-y}$ or $\frac 1{x+y}<\frac1{x-y}$.

 

[paulimerci]

1/(x+y) < 1/(x-y)

 

[haruspex]

1/(x+y) < 1/(x-y)

Right, so is F_A or F_B the greater?

 

[paulimerci]

Right, so is F_A or F_B the greater?

F_{B is greater}

 

[haruspex]

F_{B is greater}

Right. All clear now?

 

[paulimerci]

Right. All clear now?

Yes @haruspex , Thank you!

 

[PeroK]

Right, so if $x+y>x-y$ is $\frac 1{x+y}>\frac1{x-y}$ or $\frac 1{x+y}<\frac1{x-y}$.

We also need the condition $x > y$ here.

 

[haruspex]

We also need the condition $x > y$ here.

Yes, that was specified in post #31.