dislect
- 163
- 0
Hello guys,
I've had the following discussion at work:
We are currently using a suture with a nylon thread on a tissue, when the thread of the suture is tightened in a force equal to if we've put a 500 gram weight on both ends of the suture line (meaning both end are tied together to the weight).
The assumption is that in this mode, the tissue will fail with a load higher than that.
We were wondering, if the force was applied perpendicularly (direction of the screen) would the max wight change from 500 gram to another value?
Would love a direction to some equations to rationalize my first instinct of saying "No!" :-)
Thanks!
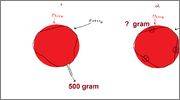
I've had the following discussion at work:
We are currently using a suture with a nylon thread on a tissue, when the thread of the suture is tightened in a force equal to if we've put a 500 gram weight on both ends of the suture line (meaning both end are tied together to the weight).
The assumption is that in this mode, the tissue will fail with a load higher than that.
We were wondering, if the force was applied perpendicularly (direction of the screen) would the max wight change from 500 gram to another value?
Would love a direction to some equations to rationalize my first instinct of saying "No!" :-)
Thanks!