Fourier Transform of an exponential function with sine modulation

[tworitdash]

I want to know the frequency domain spectrum of an exponential which is modulated with a sine function that is changing with time.

The time-domain form is,

s(t) = e^{j \frac{4\pi}{\lambda} \mu \frac{\sin(\Omega t)}{\Omega}}

Here, \mu, \Omega and \lambda are constants.

A quick implementation in MATLAB gives me the following in the frequency/velocity domain.

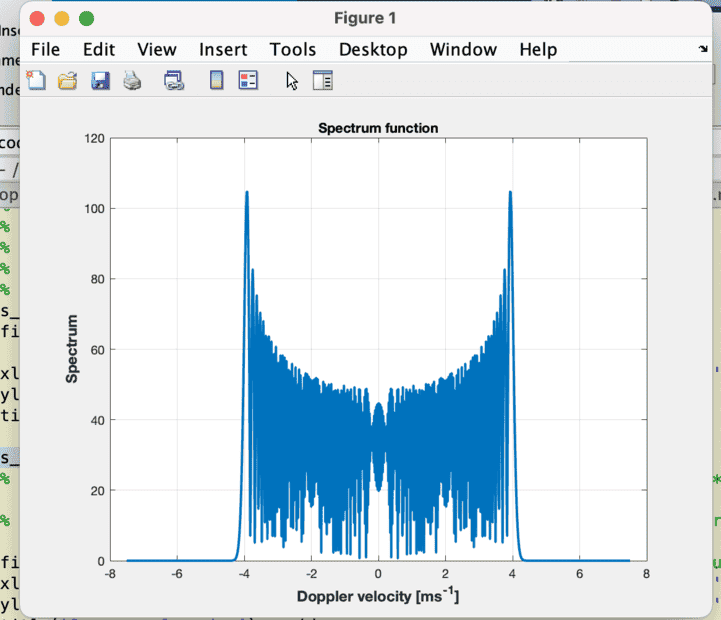
The code is given below.

[CODE lang="matlab" title="DFT"]clear;
close all;lambda = 0.03;mu = 4 * 2/lambda; % Mean Doppler frequency
Omega_rpm = 60; % in RPM
Omega = 2*pi/60 * Omega_rpm; % In rad/s
BW_deg = 1.8; % beam width in degree
BW = BW_deg * pi/180; % beam width in radian

v_amb = 7.5;PRT = 1e-3;
f_amb = 1/(2 .* PRT);p0 = 0*pi/180; % start angle
p1 = 360*pi/180; % end angle

N_BW = 1; % Number of beam widths to integrate

M = round((p1 - p0)/(BW * N_BW)); % Number of azimuth points
hs = N_BW * round(BW/Omega/PRT); % hits per scan -> Sweeps in one beamwidth

N = hs * M; % Total number of points in the time axis

th = linspace(p0, p1, N); % All the anglesphi = linspace(th(1), th(end), M); % Angle of the sectorst1 = 0:PRT:(N - 1)*PRT; % Time axis

ph_ = (2 * pi * mu .* t1);
s_ = (exp(1j .* ph_ .* (sin(eps + Omega .* t1)./(eps + Omega .* t1))));

vel_axis = linspace(-f_amb, f_amb, N); % frequency axis for the entire rotation

s_f = fftshift(fft(s_));
figure; plot(vel_axis*lambda/2, (abs(s_f)), 'LineWidth', 2); grid on;

xlabel('Doppler velocity [ms^{-1}]', 'FontSize', 12, 'FontWeight', 'bold');
ylabel('Spectrum', 'FontSize', 12, 'FontWeight', 'bold');
title('Spectrum function'); grid on;[/CODE]

I want to know what this function should look like in the spectrum domain analytically.

 

[jasonRF]

I haven't looked at your Matlab code, but the way to get an analytical expression is to use the generating function for Bessel functions
$$
e^{\frac{1}{2} z ( x - x^{-1})} = \sum_{n=-\infty}^\infty x^n J_n(z)
$$
set $x=e^{j\Omega t}$ and $z = 4\pi\mu/\lambda\Omega$ to get
$$
e^{j \frac{4\pi\mu}{\lambda\Omega} \sin(\Omega t)} = \sum_{n=-\infty}^\infty e^{j n\Omega t} J_n\left(\frac{4\pi\mu}{\lambda\Omega}\right)
$$
You can analytically work out the DFT of $e^{j n \Omega t}$ for your given sampling. I expect it will be some kind of geometric series.

jason

 

[tworitdash]

Nice Bessel function property. However, when finding the DFT I see that it is not just a geometric progression, as $n$ appears in the Bessel function order. I am writing the steps here. Correct me if I am wrong.

$$
S(v) = \sum_{n=-\infty}^{+\infty} e^{jn\Omega t} J_{n}\Big(\frac{4\pi \mu}{\lambda \Omega}\Big) e^{-j \frac{4\pi}{\lambda} n v t}
$$

$$\implies$$

$$
S(v) = \sum_{n=-\infty}^{+\infty} e^{jnt(\Omega - \frac{4\pi\mu}{\lambda})} J_{n}\Big(\frac{4\pi\mu}{\lambda \Omega}\Big)
$$

My variable for DFT is $v$.

 

[tworitdash]

Or, am I stupid enough to not see something in the above formulation?

 

[jasonRF]

The equation I gave is a continuous waveform. You first need to sample it at discrete times, then for each frequency component of the DFT you need to compute a sum. If the sample period is $T$ and we collect $L$ samples, then the $\ell^{th}$ sample of the discrete-time signal is
$$ X(\ell) = e^{j \frac{4\pi\mu}{\lambda\Omega} \sin(\Omega (\ell-1) T)} = \sum_{n=-\infty}^\infty e^{j n\Omega (\ell-1) T} J_n\left(\frac{4\pi\mu}{\lambda\Omega}\right)$$
where $\ell$ goes from $1$ to $L$, just like Matlab vectors. This is the signal you are taking the FFT of.

I hope you know that the DFT (and hence the FFT) assumes that this signal consisting of $L$ samples is one period of a periodic signal. Assuming this is what you want, the DFT in Matlab is then defined as
$$Y(k) = \sum_{\ell=1}^L X(\ell) e^{-j\frac{2 \pi}{L}(\ell-1)(k-1) } $$
where $k$ goes from $1$ to $L$. So the DFT is
$$Y(k) = \sum_{n=-\infty}^\infty J_n\left(\frac{4\pi\mu}{\lambda\Omega}\right) \sum_{\ell=1}^L e^{-j\frac{2 \pi}{L}(\ell-1)(k-1) } e^{j n\Omega (\ell-1) T} $$
The inner sum is a geometric series. Since $J_n(z)$ decreases fairly quickly once $|n| > |z|$ I expect this should be a practical formula.

jason

 

[tworitdash]

The equation I gave is a continuous waveform. You first need to sample it at discrete times, then for each frequency component of the DFT you need to compute a sum. If the sample period is $T$ and we collect $L$ samples, then the $\ell^{th}$ sample of the discrete-time signal is
$$ X(\ell) = e^{j \frac{4\pi\mu}{\lambda\Omega} \sin(\Omega (\ell-1) T)} = \sum_{n=-\infty}^\infty e^{j n\Omega (\ell-1) T} J_n\left(\frac{4\pi\mu}{\lambda\Omega}\right)$$
where $\ell$ goes from $1$ to $L$, just like Matlab vectors. This is the signal you are taking the FFT of.

I hope you know that the DFT (and hence the FFT) assumes that this signal consisting of $L$ samples is one period of a periodic signal. Assuming this is what you want, the DFT in Matlab is then defined as
$$Y(k) = \sum_{\ell=1}^L X(\ell) e^{-j\frac{2 \pi}{L}(\ell-1)(k-1) } $$
where $k$ goes from $1$ to $L$. So the DFT is
$$Y(k) = \sum_{n=-\infty}^\infty J_n\left(\frac{4\pi\mu}{\lambda\Omega}\right) \sum_{\ell=1}^L e^{-j\frac{2 \pi}{L}(\ell-1)(k-1) } e^{j n\Omega (\ell-1) T} $$
The inner sum is a geometric series. Since $J_n(z)$ decreases fairly quickly once $|n| > |z|$ I expect this should be a practical formula.

jason

Wow! now it is clear for me. Sometimes I get confused even if I know how to proceed. Thanks a lot. I will try this soon.