- #1
ponjavic
- 225
- 0
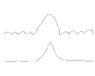
I have two signals one continuous oscillating at a high frequency and another one instantaneous at a lower frequency.
How can I use a Fourier transform to single out the low frequency one?
See at attached picture for what I am trying to do.
Edit:
Yeah by the way, data is collected in a two dimensional arrays (so discrete)
How can I use a Fourier transform to single out the low frequency one?
See at attached picture for what I am trying to do.
Edit:
Yeah by the way, data is collected in a two dimensional arrays (so discrete)
Attachments
Last edited: