Free body diagram -- Ball rotating on one arm of a Y shaped pole

[jisbon]

Homework Statement

Ball suspended on one arm of a Y shaped pole when pole rotates around vertical axis with angular velocity w, it maintains a distance h from the centre of the pole.
1) Derive an expression for the normal force on the ball.
2) Derive an expression for w

Relevant Equations

-

To start off with, I can't seem to interpret the FBD here. Here are my drawing:

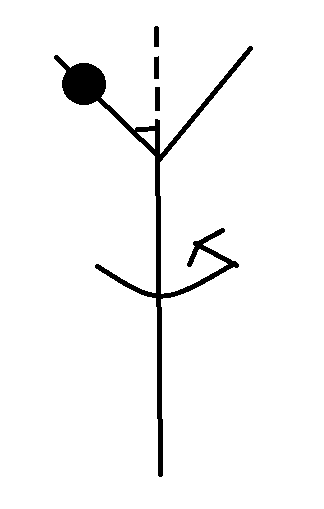
and what I interpret as.

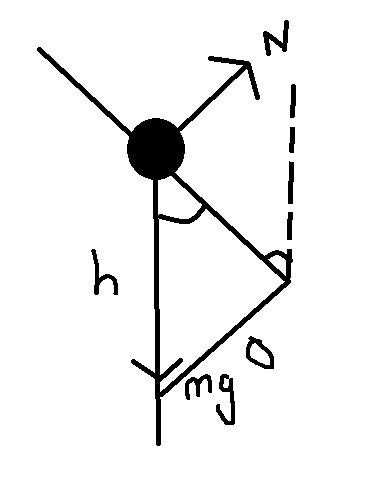
From here, I feel like I can (it's wrong obviously but I'm not sure why) state that sin theta = o/h = o/mg = N/mg , so N= mg sin theta?

Thanks

 

[kuruman]

The FBD is not enough. Write down Newton's 2nd law appropriate to this situation. Then look for the normal force.

Is the angle between the legs of the Y given? Also, is the ball actually suspended (mentioned in the statement of the problem) from a string or is it like a bead with one leg of the Y going through it as shown in your drawing??

 

[haruspex]

and what I interpret as.

View attachment 252761

Please explain this diagram.
It looks like the angled line from upper left to lower right represents the arm on which the ball is threaded, and the dashed line is the vertical continuation of the central rod. But if so, h should be either a horizontal distance or a distance down the arm to the central rod - not sure which - and I don't know what the line labeled 'o' represents.

 

[jisbon]

The FBD is not enough. Write down Newton's 2nd law appropriate to this situation. Then look for the normal force.

Is the angle between the legs of the Y given? Also, is the ball actually suspended (mentioned in the statement of the problem) from a string or is it like a bead with one leg of the Y going through it as shown in your drawing??

Angle is given to be theta. The diagram shown to be was going through, but the question states it was suspended.

Please explain this diagram.
It looks like the angled line from upper left to lower right represents the arm on which the ball is threaded, and the dashed line is the vertical continuation of the central rod. But if so, h should be either a horizontal distance or a distance down the arm to the central rod - not sure which - and I don't know what the line labeled 'o' represents.

the second picture is a zoomed-in picture of the fbd system of the first picture. O and H simply means opposite and hypotenuse

 

[haruspex]

O and H simply means opposite and hypotenuse

The diagram has h, not H, and h was given a different meaning in the problem statement. Confusing.

 

[jisbon]

The diagram has h, not H, and h was given a different meaning in the problem statement. Confusing.

Sorry, the corrected problem looks like this:

So in this case, why is it wrong to state that:

$$\begin{aligned}\sin \theta =\dfrac {a}{b}=\dfrac {a}{mg}=\dfrac {N}{mg}\\ N=mg\sin \theta \end{aligned} $$

 

[haruspex]

$$\begin{aligned}\sin \theta =\dfrac {a}{b}=\dfrac {a}{mg}=\dfrac {N}{mg}\\ N=mg\sin \theta \end{aligned} $$

First, a/(mg) makes no sense since a is a distance and mg is a force.
Second, you are overlooking that there is an acceleration.
Just do the standard process of writing the force balance equation, ΣF=ma, for each of two directions.
Given the acceleration I would suggest vertical and horizontal.