From solution to mother equation

[naviakam]

Hi
I have got two solutions to unknown equations:
1. power equation in the form y=k x(-n) where k is coefficient and n is the power
1. exponential equation of the form: y=y0+k exp(-(x-x0)/t)

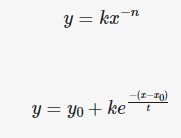
Is it possible to find the original equation/s leading to these solutions (kind a reverse engineering!)?

Best

 

[fresh_42]

Do you look for one solution for both equations with different initial conditions, or are these two different problems? If so, why don't you differentiate to find the "mother equation"?

 

[naviakam]

Do you look for one solution for both equations with different initial conditions, or are these two different problems? If so, why don't you differentiate to find the "mother equation"?

There must be one solution to both. By the way, how to differentiate in order to find the mother equation?

 

[fresh_42]

There must be one solution to both. By the way, how to differentiate in order to find the mother equation?

Your solutions can be viewed as flow through a vector field. Since one is exponential and the other one polynomial, they correspond to two different initial values, or there is a point where the behavior substantially changes, i.e. a composite function.

Is your $x$ the variable or is it itself a function of time $t$: $x=x(t)$?

 

[naviakam]

It's a variable, refers to the particle energy.

 

[martinbn]

Differentiate and substitute, for example the first one after taking derivatives is $y'=-knx^{-n-1}$. Multiply by $x$, you get $xy'=-knx^{-n}$, use the solution to find $xy'=-ny$

 

[fresh_42]

Then $y'=-knx^{-n-1}$ and $y'\cdot x +ny=0$ in the first case, and similar for the second. Could it be, that the first equation is the asymptotic behavior of the second? And is $t$ really a constant?

 

[martinbn]

Could it be, that the first equation is the asymptotic behavior of the second? And is $t$ really a constant?

One is polynomial, the other exponential!

 

[fresh_42]

One is polynomial, the other exponential!

I know.

Your solutions can be viewed as flow through a vector field. Since one is exponential and the other one polynomial, they correspond to two different initial values, or there is a point where the behavior substantially changes, i.e. a composite function.

I thought of a collection of exp curves getting flatter and flatter with $y=0$ as asymptote. Something similar to this: $y=\exp(-tx)$ with $x\to 0$ or $x\to \infty$.

 

[naviakam]

Thanks.

Ions are accelerated in a potential, the graph for number of ions versus ion energy plotted in origin and fitted. There are two plots: one is fitted with the power and the other with exponential decay in the form mentioned above (y is the number and x is the energy). We've been asked to guess the original function leading to these spectra. Amazingly, both equations seem originating from a single function!

 

[pasmith]

What form of ODE are you looking for? You can easily take ODEs satisfied by kx^n and y_0 + ke^{x/t} respectively in the form f(y,y',x) = 0 and mulitply them together to get \left(y'' - \frac{y'}{t}\right)\left(y' + \frac{ny}{x}\right) = 0 but that may not be the form of ODE you are looking for.

 

[naviakam]

What form of ODE are you looking for? You can easily take ODEs satisfied by kx^n and y_0 + ke^{x/t} respectively in the form f(y,y',x) = 0 and mulitply them together to get \left(y'' - \frac{y'}{t}\right)\left(y' + \frac{ny}{x}\right) = 0 but that may not be the form of ODE you are looking for.

1. The second term is fine but how the first term was derived?

Please show that.

2. As mentioned, capacitor discharge in a gas accelerates ions and ion spectra fitted in Origin software. The original equation must be obtained (from power and exp fits) and related to the accelerating potential.

 

[martinbn]

1. The second term is fine but how the first term was derived?
View attachment 275367
Please show that.

2. As mentioned, capacitor discharge in a gas accelerates ions and ion spectra fitted in Origin software. The original equation must be obtained (from power and exp fits) and related to the accelerating potential.

Is this a homework question?

 

[naviakam]

Is this a homework question?

Lab

 

[berkeman]

Is this a homework question?

Lab

Then it should have been posted in the Homework section of PF. I will move your thread there now. Also keep in mind that for schoolwork problems/projects, we require that you do the bulk of the work. We do not do your homework for you here.

 

[naviakam]

Then it should have been posted in the Homework section of PF. I will move your thread there now. Also keep in mind that for schoolwork problems/projects, we require that you do the bulk of the work. We do not do your homework for you here.

How this equation:

is related to the capacitor potential?

 

[haruspex]

1. The second term is fine but how the first term was derived?
View attachment 275367
Please show that.

2. As mentioned, capacitor discharge in a gas accelerates ions and ion spectra fitted in Origin software. The original equation must be obtained (from power and exp fits) and related to the accelerating potential.

It might help if you were to explain what y, x and t represent in that set-up.
In particular, is it perhaps y=y(x,t), or y=y(x(t)), or t is constant, or...?

 

[naviakam]

It might help if you were to explain what y, x and t represent in that set-up.
In particular, is it perhaps y=y(x,t), or y=y(x(t)), or t is constant, or...?

y is the number of ions, x is the energy. but t: I just fitted the curve and exponential decay fit was the best. t was given by the fit in the origin software.

 

[naviakam]

Differentiate and substitute, for example the first one after taking derivatives is $y'=-knx^{-n-1}$. Multiply by $x$, you get $xy'=-knx^{-n}$, use the solution to find $xy'=-ny$

how the equation containing y0 is differentiated?

 

[naviakam]

What form of ODE are you looking for? You can easily take ODEs satisfied by kx^n and y_0 + ke^{x/t} respectively in the form f(y,y',x) = 0 and mulitply them together to get \left(y'' - \frac{y'}{t}\right)\left(y' + \frac{ny}{x}\right) = 0 but that may not be the form of ODE you are looking for.

first term is :
y"+(1/t)Y'=0
right?

 

[haruspex]

y is the number of ions, x is the energy. but t: I just fitted the curve and exponential decay fit was the best. t was given by the fit in the origin software.

So t is an arbitrary constant? Then why doesn't the equation reduce to $y=y_0+k'e^{-\frac xt}$, where $k'=ke^\frac{x_0}t$?

 

[naviakam]

So t is an arbitrary constant? Then why doesn't the equation reduce to $y=y_0+k'e^{-\frac xt}$, where $k'=ke^\frac{x_0}t$?

then what is the next step?

 

[haruspex]

then what is the next step?

I see nothing better than has already been suggested, @pasmith's post #11, with your sign correction in post #20. But it does look very artificial and unconvincing.

I'm not sure I understand your situation. If these equations come from curve fitting, how can you be sure they really are of the form you specify?
What happens if you insist on one form, either power or exponential, and fit both sets of data to that?

I am also surprised that whatever software you used to produce the exponential fit generated three constants when two would have sufficed.

 

[naviakam]

I see nothing better than has already been suggested, @pasmith's post #11, with your sign correction in post #20. But it does look very artificial and unconvincing.

I'm not sure I understand your situation. If these equations come from curve fitting, how can you be sure they really are of the form you specify?
What happens if you insist on one form, either power or exponential, and fit both sets of data to that?

I am also surprised that whatever software you used to produce the exponential fit generated three constants when two would have sufficed.

Then regarding to post #11: how to correlate this equation with the potential? I want to find type of potential that generated this equation!

 

[naviakam]

in other word possible to draw ion spectra (of the form above) from potential?

 

[pasmith]

I assume the physics will tell you which functions can be potential functions, and what parameters they have which you can vary to fit your data. You should not be trying to fit your data to exponential or power laws unless the physics tells you to expect those (because a potential of a particular form will give you a curve which looks like that).

You say that this is lab work. Does your assignment include instructions on how to go about analysing your results to obtain the potential? Has this been covered in lectures? What does your textbook have to say on the matter?

 

[naviakam]

this is the lab for a plasma course. we discharge capacitor in a gas and measure the ion spectrum. then we have been asked to correlate the spectra with governing potential!

 

[naviakam]

I assume the physics will tell you which functions can be potential functions, and what parameters they have which you can vary to fit your data. You should not be trying to fit your data to exponential or power laws unless the physics tells you to expect those (because a potential of a particular form will give you a curve which looks like that).

You say that this is lab work. Does your assignment include instructions on how to go about analysing your results to obtain the potential? Has this been covered in lectures? What does your textbook have to say on the matter?

is it possible at all to correlate this equation with the potential function?

 

[Fred Wright]

First, there is no "mother equation". I am going to make some assumptions about your experiment.
1. You have a Langmoir probe inserted in the plasma connected to a power supply to bias it to negative/positive voltages.
2. You obtain a current-voltage plot.
3. The plot has three regions:
Region I (Townsend discharge region):
In this region the probe is negatively biased; electrons are rejected from the probe and ions are collected. The ion's current that passes area $A_p$ in the plasma is linked to both ion density and velocity,
$$
J_p =\frac{I_p}{A_p}=\frac{n_iev_{th}}{4}=\frac{n_ie}{4}\left (\frac{2K_B T}{m_i} \right )^{\frac{1}{2}}
$$
$J_p$ is ion current density, $I_p$ is plasma current, $n_i$ is ion density, $v_{th}$ is thermal velocity, $e$ is electric charge, $K_B$ is Boltzmann's constant, $m_i$ is ion mass, and $T$ is absolute temperature. Does this equation's form look familiar to you?

Region II (glow discharge region):
Rendering the value of V less negative will compel the probe to collect both ions and electrons (high thermal energy). As $V$ is made more positive, the collected ions and electrons are expected to cancel (or balance) each other out. This probe-plasma potential, $V_f$ is called the floating potential. In the event of thermalized plasma, this voltage is $\frac{1}{K_BT}$ (expressed in eV). When $V$ is increased $V_f$ electron current increases.The resulting current is exponentially related to $V$. In region II, the electron current are defined by:
$$
J_e=\frac{I_e}{A_p}=\frac{n_eev_{th}}{4}e^{\frac{-eV}{K_BT_e}}
$$
$T_e$ is the electron temperature. Does this equation look familiar to you?

Region III
In this region the plasma current saturates at a plasma space potential value $\psi_p$, caused by the space charge limitation during current collection.

 

[naviakam]

First, there is no "mother equation". I am going to make some assumptions about your experiment.
1. You have a Langmoir probe inserted in the plasma connected to a power supply to bias it to negative/positive voltages.
2. You obtain a current-voltage plot.
3. The plot has three regions:
Region I (Townsend discharge region):
In this region the probe is negatively biased; electrons are rejected from the probe and ions are collected. The ion's current that passes area $A_p$ in the plasma is linked to both ion density and velocity,
$$
J_p =\frac{I_p}{A_p}=\frac{n_iev_{th}}{4}=\frac{n_ie}{4}\left (\frac{2K_B T}{m_i} \right )^{\frac{1}{2}}
$$
$J_p$ is ion current density, $I_p$ is plasma current, $n_i$ is ion density, $v_{th}$ is thermal velocity, $e$ is electric charge, $K_B$ is Boltzmann's constant, $m_i$ is ion mass, and $T$ is absolute temperature. Does this equation's form look familiar to you?

Region II (glow discharge region):
Rendering the value of V less negative will compel the probe to collect both ions and electrons (high thermal energy). As $V$ is made more positive, the collected ions and electrons are expected to cancel (or balance) each other out. This probe-plasma potential, $V_f$ is called the floating potential. In the event of thermalized plasma, this voltage is $\frac{1}{K_BT}$ (expressed in eV). When $V$ is increased $V_f$ electron current increases.The resulting current is exponentially related to $V$. In region II, the electron current are defined by:
$$
J_e=\frac{I_e}{A_p}=\frac{n_eev_{th}}{4}e^{\frac{-eV}{K_BT_e}}
$$
$T_e$ is the electron temperature. Does this equation look familiar to you?

Region III
In this region the plasma current saturates at a plasma space potential value $\psi_p$, caused by the space charge limitation during current collection.

diagnostic is a plastic plate (CR-39) placed above a cylindrical magnet. ions deflected passing through the magnet based on their energy and form tracks on the plate.