NoWay1
- 5
- 0
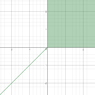
The equation is x-|x|=y-|y| and I need to make a graph for it.
So I thought I should solve it by breaking it down to 4 different equations, which would be -
x - x = y - y => 0=0
x - x = y + y => 0=2y => y = 0
x + x = y - y => 2x=0 => x = 0
x + x = y + y => 2x=2y => x = y
But this isn't correct, riight? I don't know what else to do, kinda lost here.
Would love some help, thanks.
So I thought I should solve it by breaking it down to 4 different equations, which would be -
x - x = y - y => 0=0
x - x = y + y => 0=2y => y = 0
x + x = y - y => 2x=0 => x = 0
x + x = y + y => 2x=2y => x = y
But this isn't correct, riight? I don't know what else to do, kinda lost here.
Would love some help, thanks.