- #1
olgerm
Gold Member
- 533
- 35
I was thinking about an experiment to demonstrate gravitomagnetic effect. I did my calculations using gravitomagnetic model. It is not as accurate as general relativity, but GR should give similar predictions. I do not know if it would be possible to to this experiment in real life(are there enougth accurate sensors and tought materials).
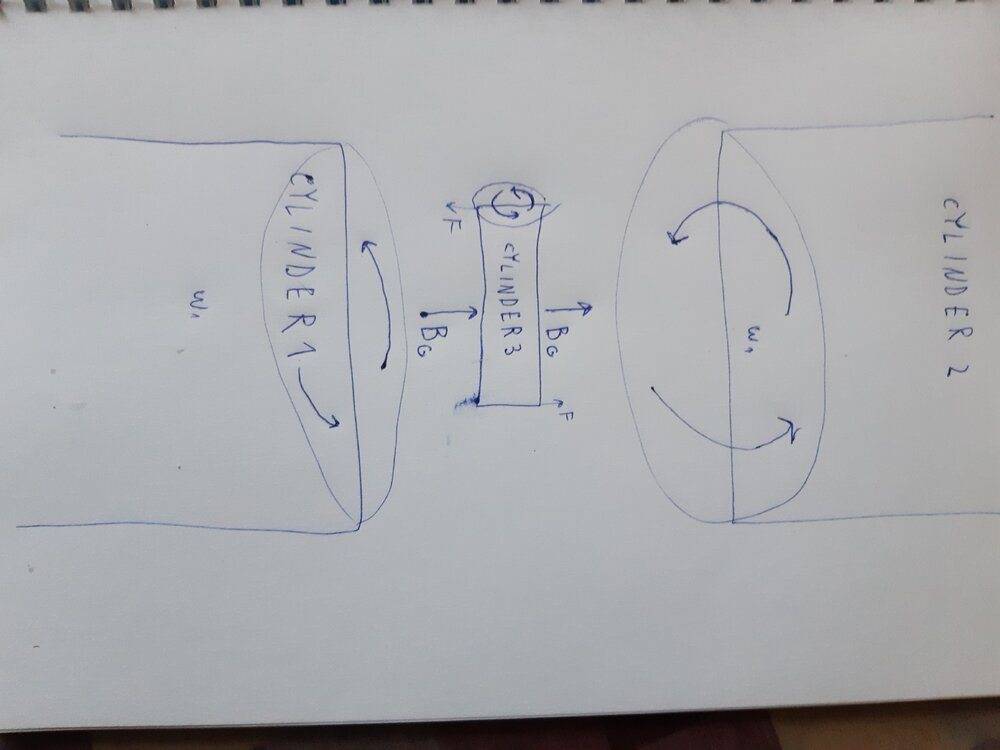
installations consists of three spinning cylinders. first to cylinders are for creating a magnetic field. last one is for detecting gravitomagnetic field. last cylinder under axis 90 degrees angle compared to first two cylinders.
gravitimagnetic field created by first two cylinders right between the cylinders: ##B_G=\frac{\mu_G \omega_1 \rho_1 (r_2^2-r_1^2)}{2}##
torque on third cylinder because of gravitomagnetic effect is crosswise to its angular speed and angular speed of first two cylinders.
##\tau=\frac{2\pi \rho_3 (R_2^4-R_1^4) \omega_3 B_G}{2}=\frac{\mu_G \omega_3 \rho_3 (r_2^2-r_1^2) 2\pi \rho_1 (R_2^4-R_1^4) \omega_1}{4}##
What you think what is the highest value for ##B_G## and ##\tau## we could practically get?
Derivation of equations
gravitimagneticfield:
I used formula ##B=\mu n I## from http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html. Using similarities between gravitomagnetism and electromagnetism: ##B_G=\mu_G n I_G=\frac{d^2m}{dl dt} \mu_G=\mu_G \frac{d^2m}{dl dt}=\mu_G \int_{r_1}^{r_2}(dr \rho v(r))=\mu_G \int_{r_1}^{r_2}(dr \rho \omega r)=\mu_G \rho \omega \int_{r_1}^{r_2}(dr r)=\frac{\mu_G \rho \omega (r_2^2-r_1^2)}{2}##
magnetic moment:
I used formula ##m ={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,{\rm {d}}V## from https://en.wikipedia.org/wiki/Magnetic_moment .
using similarities between gravitomagnetism and electromagnetism: ##M_G={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,{\rm {d}}V##
##|M_G|={\frac {1}{2}}\iiint _{V}r \frac{d^2m}{dl dt} dV=\frac {1}{2}\iiint _{V}r \rho v dV=\frac {1}{2}\int_V r^2 \rho \omega dV=\frac {1}{2}\int_{R_1}^{R_2}h r^2 \rho \omega 2\pi r dr=\frac {h \rho \omega 2\pi}{2}\int_{R_1}^{R_2}(r^3 dr)=\frac{2\pi \rho (R_2^4-R_1^4) h \omega_2}{8}=\frac{2\pi\rho(R_2^4-R_1^4)h\omega_2}{8}##.
torque:
I used formula ##\tau=M\times B## from https://en.wikipedia.org/wiki/Magnetic_moment
using similarities between gravitomagnetism and electromagnetism: ##\tau=4 M_G\times B_G##
installations consists of three spinning cylinders. first to cylinders are for creating a magnetic field. last one is for detecting gravitomagnetic field. last cylinder under axis 90 degrees angle compared to first two cylinders.
gravitimagnetic field created by first two cylinders right between the cylinders: ##B_G=\frac{\mu_G \omega_1 \rho_1 (r_2^2-r_1^2)}{2}##
- ##\omega_1## is angular speed of 1. and 2. cylinder.
- ##\mu_G##is gravitomagnetic constant ##\mu_G=\frac{2 2\pi G}{c^2} \approx 9.33\ 10^{-27} N/kg^2 s^2=9.33\ 10^{-27} s/kg##
- ##\rho_1## is density of 1. and 2. cylinder.
- ##r_2## is 1. and 2. cylinders outer radius.
- ##r_1## is 1. and 2. cylinders inner radius.
torque on third cylinder because of gravitomagnetic effect is crosswise to its angular speed and angular speed of first two cylinders.
##\tau=\frac{2\pi \rho_3 (R_2^4-R_1^4) \omega_3 B_G}{2}=\frac{\mu_G \omega_3 \rho_3 (r_2^2-r_1^2) 2\pi \rho_1 (R_2^4-R_1^4) \omega_1}{4}##
- ##R_1## is 3. cylinders inner radius.
- ##R_2## is 3. cylinders outer radius.
- ##\rho_3## is density of 3. cylinder.
- ##\omega_3## is angular speed of 3. cylinder.
What you think what is the highest value for ##B_G## and ##\tau## we could practically get?
Derivation of equations
gravitimagneticfield:
I used formula ##B=\mu n I## from http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html. Using similarities between gravitomagnetism and electromagnetism: ##B_G=\mu_G n I_G=\frac{d^2m}{dl dt} \mu_G=\mu_G \frac{d^2m}{dl dt}=\mu_G \int_{r_1}^{r_2}(dr \rho v(r))=\mu_G \int_{r_1}^{r_2}(dr \rho \omega r)=\mu_G \rho \omega \int_{r_1}^{r_2}(dr r)=\frac{\mu_G \rho \omega (r_2^2-r_1^2)}{2}##
magnetic moment:
I used formula ##m ={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,{\rm {d}}V## from https://en.wikipedia.org/wiki/Magnetic_moment .
using similarities between gravitomagnetism and electromagnetism: ##M_G={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,{\rm {d}}V##
##|M_G|={\frac {1}{2}}\iiint _{V}r \frac{d^2m}{dl dt} dV=\frac {1}{2}\iiint _{V}r \rho v dV=\frac {1}{2}\int_V r^2 \rho \omega dV=\frac {1}{2}\int_{R_1}^{R_2}h r^2 \rho \omega 2\pi r dr=\frac {h \rho \omega 2\pi}{2}\int_{R_1}^{R_2}(r^3 dr)=\frac{2\pi \rho (R_2^4-R_1^4) h \omega_2}{8}=\frac{2\pi\rho(R_2^4-R_1^4)h\omega_2}{8}##.
torque:
I used formula ##\tau=M\times B## from https://en.wikipedia.org/wiki/Magnetic_moment
using similarities between gravitomagnetism and electromagnetism: ##\tau=4 M_G\times B_G##