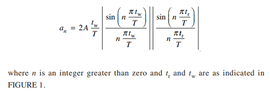Harmonic Amplitudes - 3rd & 101st

[Jason-Li]

Homework Statement

A low voltage digital device has a low state of 0 V and a high state of
1.8 V. It generates a signal train of high pulses at a rate of 1 MHz, these
pulses having a 10 ns width and transition times of 100 ps.

Determine the amplitudes of the third and 101st harmonics.

Relevant Equations

As below:

I have attempted the question using the large formula here with figures from the waveform with n as 3 & 101:

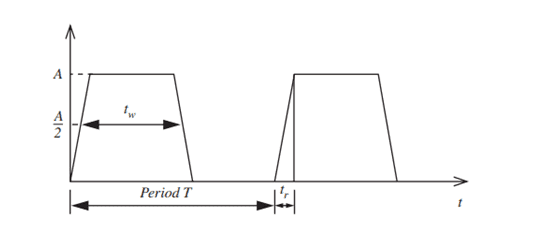
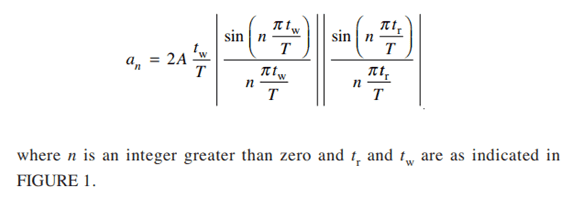
however I think that the large formula is for the total waveform encompassing all harmonics as the 3rd and 101st harmonic amplitudes are very similar 10.9662222 *10^-6V for the 3rd harmonic and 10.9606221 *10^-6V for the 101st harmonic.

I have since tried to use the formula for individual sinusoidal components:

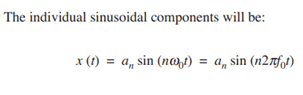
How would I go about using this formula? Would I substitute 0 or alternatively a figure such as 5ns so 5*10^-9s then rearrange for An like below:

x(t) = An * sin (n*2*pi*f0*t)

x(5*10^-9) = An * sin (3*2*pi*1000000*5*10^-9)
x(5*10^-9) = An * sin (0.03)

Not sure how to progress from here... a little pointer would be much appreciated! !

 

[.Scott]

Edit: deleted - this was a worthless clue.

 

[Jason-Li]

Your function is not unlike the delta function.
Are you familiar with the Fourier Transform? If so, what is the Fourier Transform of the delta function?
If not, I will have to think up another clue.

Thanks for your reply Scott

Apologies I am not familiar with it no. Had a quick look and definitely not seen it before I don't think.

Could I take the formula
x(t) = An*Sin(n*2*π*f*t)
And integrate it between say 0 & 1 which would return:

Which I would then enter my figures into for f & n - again then unsure where to take it from here

 

[Jason-Li]

Your function is not unlike the delta function.
Are you familiar with the Fourier Transform? If so, what is the Fourier Transform of the delta function?
If not, I will have to think up another clue.

I think the question is looking for a "simple" answer as it is stated in our learning materials (figure 1 is the trapezoidal waveform) :

 

[.Scott]

Edit: On closer examination - those values should be about the same as for a square wave.

 

[Jason-Li]

I am not surprised that you got about the same value for the 3rd and 101st harmonics.

Due to them both being odd waves? Still not sure how the high state can be 1.8V but the 3rd harmonic is so low at 10.9662222 *10^-6V if I've used the formula correctly

 

[.Scott]

There are two equations for this. I am looking at the wiki page for "Pulse wave".
It's also slide 28 of this.

You basically have a pulse wave with a period of 1usec, and a duty cycle of 1% and amplitude 1.8.

From slide 28:
$g(t) = dA + \sum_{n=1}^{\infty} { \frac{2A}{\pi n} sin(\pi dn) cos(2\pi fnt) }$

This is what I get:

So 3rd harmonic is: $\frac{3.6}{3 \pi} sin(0.03 \pi) cos(2\pi f3t)$
So 101st harmonic is: $\frac{3.6}{101 \pi} sin(1.01 \pi) cos(2\pi f101t)$

But we are only interested in the amplitudes of these harmonics:
So amplitude of 3rd harmonic is: $\frac{3.6}{3 \pi} sin(0.03 \pi) = 0.036$
So amplitude of 101st harmonic is: $\frac{3.6}{101 \pi} sin(1.01 \pi) = -0.000356$

(use the absolute values)

 

[Jason-Li]

There are two equations for this. I am looking at the wiki page for "Pulse wave".
It's also slide 28 of this.

You basically have a pulse wave with a period of 1usec, and a duty cycle of 1% and amplitude 1.8.

From slide 28:
$g(t) = dA + \sum_{n=1}^{\infty} { \frac{2A}{\pi n} sin(\pi dn) cos(2\pi fnt) }$

This is what I get:

So 3rd harmonic is: $\frac{3.6}{3 \pi} sin(0.03 \pi) cos(2\pi f3t)$
So 101st harmonic is: $\frac{3.6}{101 \pi} sin(1.01 \pi) cos(2\pi f101t)$

But we are only interested in the amplitudes of these harmonics:
So amplitude of 3rd harmonic is: $\frac{3.6}{3 \pi} sin(0.03 \pi) = 0.036$
So amplitude of 101st harmonic is: $\frac{3.6}{101 \pi} sin(1.01 \pi) = -0.000356$

(use the absolute values)

Scott, this it probably a better explanation and linked materials than all of my learning materials combined thank you, there isn't even mention of duty cycles in the material...

So as per that slides the Sin is just a "scaling factor" for the amplitude - is that why I can just ignore the cos in this instance and whatever figure is with sin will be the amplitude?

Also, I can't see why the learning materials would give me a method that is so unfleshed out... seems to be a theme with them to be honest

 

[.Scott]

So as per that slides the Sin is just a "scaling factor" for the amplitude - is that why I can just ignore the cos in this instance and whatever figure is with sin will be the amplitude?

The cosine term with the "t" in it will always give you a value in the range of 1 to -1. So the other terms (the ratio and the cosine) for the amplitude.

 

[DaveE]

is that why I can just ignore the cos in this instance and whatever figure is with sin will be the amplitude?

When they ask about the amplitude of a particular harmonic, they are telling you to ignore the sinusoidal oscillation at that harmonic frequency. There's a better explanation in maths about Fourier series and the orthogonality of sinusoidal functions that I'll skip over for now. However, the "amplitude" of $A⋅sin(\omega t)$ is $A$ (usually, see below).

When people ask about amplitudes, they should qualify their question with amplitude of what, measured how? This part of the question is often assumed, i.e. your supposed to figure out what they are asking by the context. This is sloppy, but it is they way humans communicate. For example, many people would give you the RMS value $\frac{A}{\sqrt{2}}$ instead, depending on the context of the problem.

 

[Jason-Li]

The cosine term with the "t" in it will always give you a value in the range of 1 to -1. So the other terms (the ratio and the cosine) for the amplitude.

Ah so the cosine is indicate how far into the cycle the wave is ranging effectively across the y-axis between -1 & 1?

When they ask about the amplitude of a particular harmonic, they are telling you to ignore the sinusoidal oscillation at that harmonic frequency. There's a better explanation in maths about Fourier series and the orthogonality of sinusoidal functions that I'll skip over for now. However, the "amplitude" of $A⋅sin(\omega t)$ is $A$ (usually, see below).

When people ask about amplitudes, they should qualify their question with amplitude of what, measured how? This part of the question is often assumed, i.e. your supposed to figure out what they are asking by the context. This is sloppy, but it is they way humans communicate. For example, many people would give you the RMS value $\frac{A}{\sqrt{2}}$ instead, depending on the context of the problem.

Yeah that is why I was struggling to understand I think because "$A⋅sin(\omega t)$ is $A$" I was seeing this simplified as $A⋅B$ so how could amplitude (A) be effectively what B mutliplies out as. For instance if $sin(\omega t)$ is 10 then I would have $A⋅10$ which wouldn't help with the actual figure of A? On a side note, would either of you be able to shed a light on why the large formula at the top of the page returns different answers to the calculations carried out by .Scott ?

 

[.Scott]

On a side note, would either of you be able to shed a light on why the large formula at the top of the page returns different answers to the calculations carried out by .Scott ?

The problem you were given was a trapezoidal wave. What I gave you was for a rectangular wave. What I gave you is a good sanity check - the differences between the solutions should be relatively small. So when you succeed in solving the trapezoid case, you can compare them to determine if you are in the right ball park.

 

[Jason-Li]

The problem you were given was a trapezoidal wave. What I gave you was for a rectangular wave. What I gave you is a good sanity check - the differences between the solutions should be relatively small. So when you succeed in solving the trapezoid case, you can compare them to determine if you are in the right ball park.

Ah of course that makes sense. I can see the first part of the large equation does again equal 0.036 so that would mean that the two other functions would dictate the amplitudes of each wave and in terms of being trapezoidal as the first part of the function has no mention of frequency or which harmonic?

2A⋅t_w/T = 2*1.8*10*10^-9/1*10^-6= 0.036

Then for the 3rd harmonic adjusting frequency to 3Mhz which also changes t_w & T & t_r to 3.3ns, 333ns & 33ps respectively.

This still returns the same answer as I got previously as the final equation will boil down to:

a_n = 0.036*0.0174532848*0.01745329252 = 10.96*10^{-6 V}

How can the amplitude can be so much lower than if it was a purely square wave like you calculated?

 

[Jason-Li]

The problem you were given was a trapezoidal wave. What I gave you was for a rectangular wave. What I gave you is a good sanity check - the differences between the solutions should be relatively small. So when you succeed in solving the trapezoid case, you can compare them to determine if you are in the right ball park.

Edited - I was an idiot and didn't use radians.

@.Scott & @DaveE I think I have the correct answer now - thank you both! All of this has helped it click.