Astrocyte
- 15
- 4
- Homework Statement
- Find Cp-Cv for Van Der Waals' Gas
- Relevant Equations
- Grand Partition Function, Grand potential.
In our class, we're using Wassermann's Thermal physics as textbook.
I always try to solve all question which included in Text book.
But sometime when I meet a problem that look like easy but actually hard, I'm so embarrassed.
This problem do also.
First, in the textbook grand potential for van der Waals' gas is
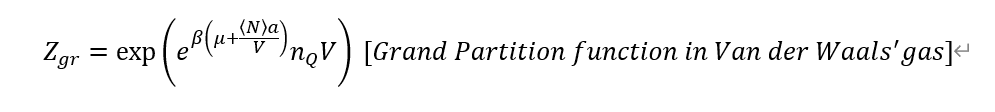
Next, I calculated routinely, but it's so complex.
The internal energy come from previous problem. I guess it's right.
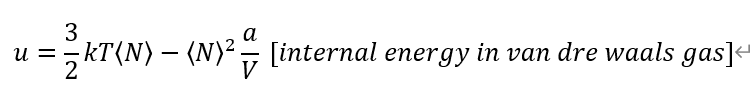
From definition of each Heat capacities. And, Entropy from Grand potential Omega.
I used previous calculation on average particle number <N>.
<N>=exp( \beta (\mu + <N>a/V))*n_Q*V
Also, n_Q is quantum concentration, which come from Ideal gas partition function, and define (m/(2*\pi*\hbar^2*\beta)^3/2
So, n_Q also depends on \beta or Temperature T.
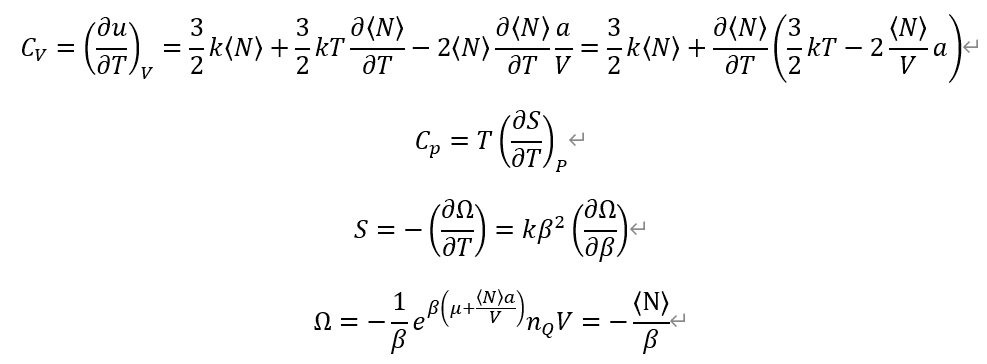
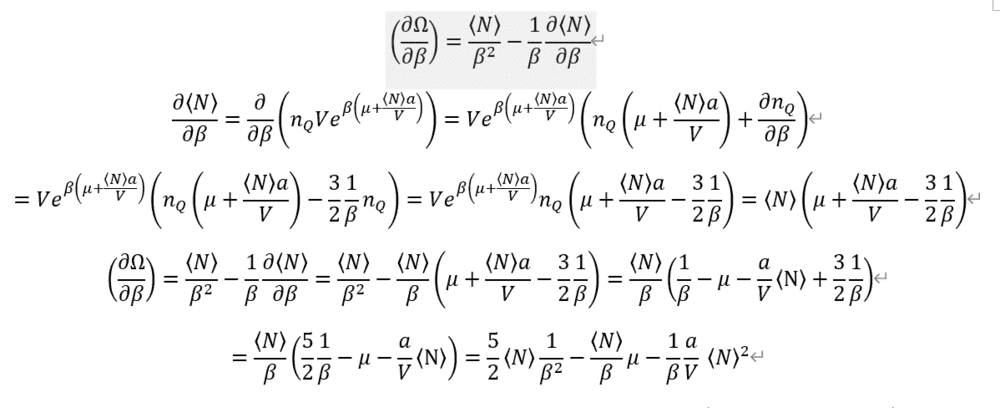
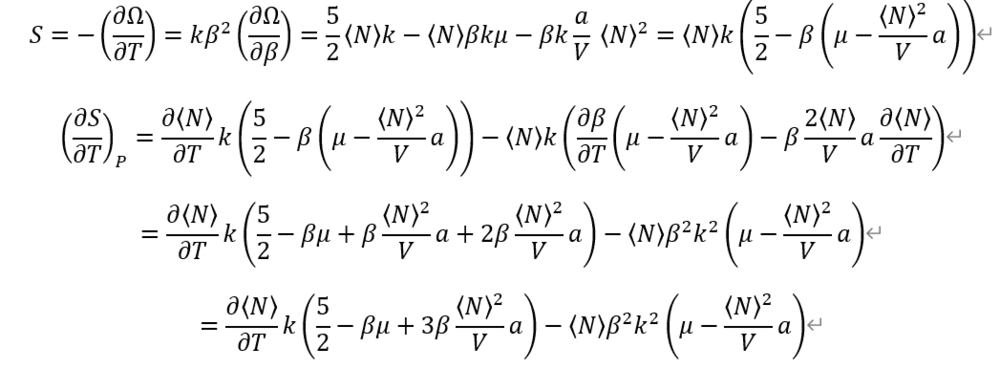
Entropy is so complex.
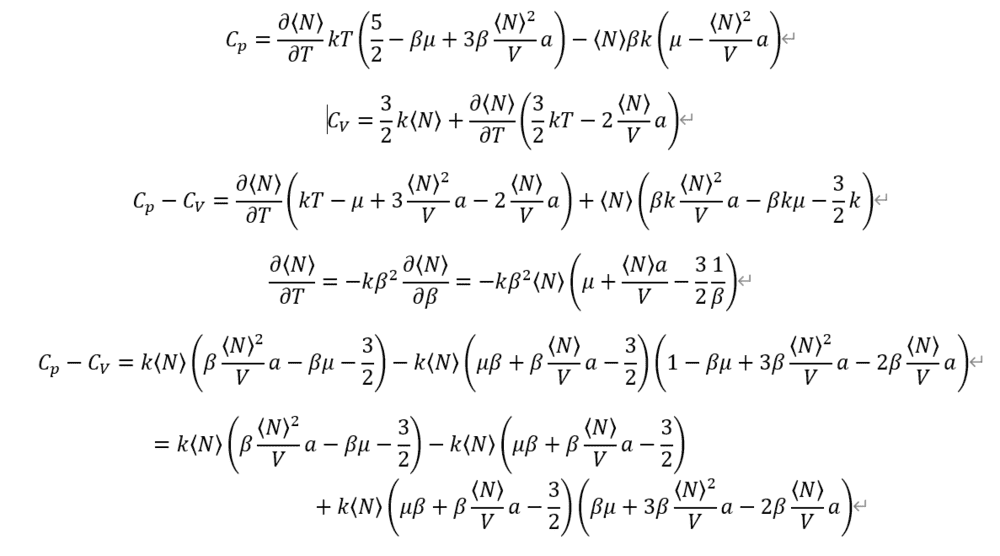
And I given up, because it's so complex for calculating by hand.
Where am I wrong?
I always try to solve all question which included in Text book.
But sometime when I meet a problem that look like easy but actually hard, I'm so embarrassed.
This problem do also.
First, in the textbook grand potential for van der Waals' gas is
Next, I calculated routinely, but it's so complex.
The internal energy come from previous problem. I guess it's right.
From definition of each Heat capacities. And, Entropy from Grand potential Omega.
I used previous calculation on average particle number <N>.
<N>=exp( \beta (\mu + <N>a/V))*n_Q*V
Also, n_Q is quantum concentration, which come from Ideal gas partition function, and define (m/(2*\pi*\hbar^2*\beta)^3/2
So, n_Q also depends on \beta or Temperature T.
Entropy is so complex.
And I given up, because it's so complex for calculating by hand.
Where am I wrong?