Height at which pilot must pull out of dive before hitting 5g

[negation]

Homework Statement

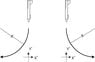
A jet is diving vertically downwards at 1200kmh^-1. If the pilot can withstand a max acceleration of 5g before losing consciousness, at what height must the plane start a quarter turn to pull out of the dive.
Assume the speed remains constant.

The Attempt at a Solution

I do not understand the question fully. Could someone give me a leg-up?

 

[rcgldr]

I would assume the problem is asking what is the lowest height so that the pilot can pull ouf of the dive without hitting the ground or exceeding 5 g's. I would assume the 5 g limit needs to take the effect of gravity into account.

 

[BvU]

Oh boy, a lot of parallel questions. What do you think is meant when you read "quarter" turn ?

 

[negation]

Oh boy, a lot of parallel questions. What do you think is meant when you read "quarter" turn ?

That the pilot makes a pi/2 turn?

 

[negation]

I drew a circle for this and take the radius (the -y component) as the height along which the pilot travels before making the quarter turn.
But beyond which, I have no idea.

 

[BvU]

Good. Maybe, because ambiguous. Turning can be done many ways with a jet plane. With a side view and a top view, which kind of turn do you mean ?

 

[negation]

Good. Maybe, because ambiguous. Turning can be done many ways with a jet plane. With a side view and a top view, which kind of turn do you mean ?

The side view.

 

[BvU]

I see no turn, but you made a good choice. It was more or less stipulated in the word "pull" in the OP. Which way do you want the guy to turn ?

 

[BvU]

If he does his thing right, what g does he feel after this scary emergency measure ?

 

[HallsofIvy]

I presume you know that in making a circular turn of radius r, at speed v, the inward acceleration has magnitude $\frac{v^2}{r}$ so "centrifugal force" on the pilot will be $\frac{v^2m}{r}$ where m is the mass of the pilot. I'm not clear whether the "5gs" acceleration the pilot can stand is to include the pilots weight or not. If it is not, then set $\frac{v^2m}{r}= 5mg$ and solve for r. If it is, set $\frac{v^2m}{r}= 4mg$ (subtracting the pilots weight, mg) and solve for r. Of course, if he is making a vertical circle of radius r, he had better be at least "r" above the ground to avoid hitting the ground! We can write a circle of radius r, as parametric equations x= r cos(\omega t), y= r sin(\omega t). differentiating, v_x= -r\omega sin(\omega t), v_y= r\omega cos(\omega t). The acceleration is given by, differentiating again, a_x= -r\omega^2 cos(\omega t), a_y= -r\omega^2 sin(\omega t).

The speed at each instant is given by \sqrt{v_x^2+ v_y^2}= \sqrt{r^2\omega^2}= r\omega= v so we must have \omega= v/r. Then the acceleration is given by a_x= -(v^2/r) cos(\omega t), a_y= -(v

 

[negation]

I see no turn, but you made a good choice. It was more or less stipulated in the word "pull" in the OP. Which way do you want the guy to turn ?

Let's suppose he turns in the -x direction

 

[HallsofIvy]

I presume you know that making a circle of radius r, at speed v, there must be a centripetal force of magnitude $mv^2/r$. I don't know whether the pilots own weight is included in the "5 gs" or not. If it is not then we must have $mv^2/r= 5mg$. If it is, then subtract 1 mg for his weight to get $mv^2/r= 4mg$.

Solve one of those for r. Of course, his initial height, before making that loop must be at least "r" to avoid hitting the ground!

 

[BvU]

Which way is that ? Or was there a coordinate system present already ?

 

[BvU]

@HallsofIvy, don't spoil this! With all due respect, of course...

 

[BvU]

If I were at the controls, I'd prefer the one on the right. Flying upside down at height zero is riskier than head up. Agree?

 

[HallsofIvy]

@HallsofIvy, don't spoil this! With all due respect, of course...

I'm sorry, I foolishly thought we were being serious. I clearly did not read the responses carefully enough.

 

[BvU]

Negation, are you comfortable with the equations for circular motion at constant speed?
All you asked for was a leg-up and now we already have 17 posts!

 

[negation]

Negation, are you comfortable with the equations for circular motion at constant speed?
All you asked for was a leg-up and now we already have 17 posts!

To some degree, I am.

I conceive of a circle with the origin (0,0) and of radius, r. The plane begins from (r,0) and takes the path of an arc length in quadrant 4. At point (-r,0), it begins moving horizontally.
In moving along the arc length, the acceleration changes and I right? And we want the g value to be lesser to or equal to 5g along the arc length.

a = g = v^2/ r

5(9.8) = 333^2/r
r = 2263m

r represents the height at which the pilot must make the turn along the arc length cojoining (-r,0) and (0-r).
Is this it?

 

[negation]

If I were at the controls, I'd prefer the one on the right. Flying upside down at height zero is riskier than head up. Agree?

Yes, this was what I have in mind.
Although, the left one was what I had exactly in mind. But both diagrams are essentially parallel model of one another.

 

[BvU]

You are absolutely right: concerning the physics exercise they are equivalent. But pilot's g-resistance applies to downward g forces: you survive/stay conscious longer with those than with the blood running to your head. (I think -- will ask my son who is in the business)

My battle plan for you was to focus on the worst case: the end of the quarter circle. Then centripetal force and upward force from the gravity pushing the pilot down into the ejector seat align and therefore the magnitude of the sum is at a maximum. This would leave 4g for the centripetal force to execute the 'turn', and the expressions etc. were already posted.

You will do fine on this one, I am sure. Look forward to the next encounter.

 

[negation]

You are absolutely right: concerning the physics exercise they are equivalent. But pilot's g-resistance applies to downward g forces: you survive/stay conscious longer with those than with the blood running to your head. (I think -- will ask my son who is in the business)

My battle plan for you was to focus on the worst case: the end of the quarter circle. Then centripetal force and upward force from the gravity pushing the pilot down into the ejector seat align and therefore the magnitude of the sum is at a maximum. This would leave 4g for the centripetal force to execute the 'turn', and the expressions etc. were already posted.

You will do fine on this one, I am sure. Look forward to the next encounter.

So my answer is right?

 

[BvU]

Actually, I missed your answer at first: it was at the bottom of page 1 of 2 and I picked up at post #19.
Did you read my post #20 ? After passing point Q the pilot experiences 1 g. That is also there just before point Q, so the total in the case of your answer would be 6 g. The guy might pass out!

There is a point of discussion possible here: is the 5g absolute or in excess of normal on-the-ground gravitational acceleration. I agree with rcgldr that it is absolute. That way you can 'easily' calculate that he can make a horizontal circle of radius 2300 m, but for a looping he has to be more careful, especially in the lower half.

So

So my answer is right?

I would say most likely not. But you know what to do.

 

[negation]

Actually, I missed your answer at first: it was at the bottom of page 1 of 2 and I picked up at post #19.
Did you read my post #20 ? After passing point Q the pilot experiences 1 g. That is also there just before point Q, so the total in the case of your answer would be 6 g. The guy might pass out!

There is a point of discussion possible here: is the 5g absolute or in excess of normal on-the-ground gravitational acceleration. I agree with rcgldr that it is absolute. That way you can 'easily' calculate that he can make a horizontal circle of radius 2300 m, but for a looping he has to be more careful, especially in the lower half.

So I would say most likely not. But you know what to do.

I'm a little confused. At point g, the pilot experiences 1g if he travels horizontally
from point Q (0,-r)onward. Between point (-r,0) and (0,-r), is the pilot experiencing 5g or 6g? I'm still quite hazy. And what do we have to take into account the 1g of the pilot?

 

[negation]

You are absolutely right: concerning the physics exercise they are equivalent. But pilot's g-resistance applies to downward g forces: you survive/stay conscious longer with those than with the blood running to your head. (I think -- will ask my son who is in the business)

My battle plan for you was to focus on the worst case: the end of the quarter circle. Then centripetal force and upward force from the gravity pushing the pilot down into the ejector seat align and therefore the magnitude of the sum is at a maximum. This would leave 4g for the centripetal force to execute the 'turn', and the expressions etc. were already posted.

You will do fine on this one, I am sure. Look forward to the next encounter.

If the centripetal force is 4g, then would the mathematical reasoning 4g = v^2/r work?

 

[BvU]

If the centripetal force is 4g, then would the mathematical reasoning 4g = v^2/r work?

For the record: the force needed for the circle trajectory is 4mg towards the centre. 4g is an acceleration. And yes, the acceleration towards the centre of a circular trajectory is v²/r

Between point (-r,0) and (0,-r), is the pilot experiencing 5g or 6g? I'm still quite hazy. And what do we have to take into account the 1g of the pilot?

While going straight down at constant speed, the pilot experiences 1g downward. This is a vector.
As soon as he pulls the wheel (or what do they call it) towards him, a uniform circular motion sets in that requires 4g of acceleration towards the centre. His seat provides the force required for that acceleration. Also a vector, initially pointing to the right. So initially he feels an acceleration of 1 g down, 4g to the right. √17 magnitude total. Gradually going towards 1 g down and 4 g down as well just before point q. Magnitude now 5 g (same direction). He can stand that as per given in the OP. If he's smart he pulls up a little longer, haha. The moment he is going straight again, he experiences 1 g towards the center of the earth.

 

[negation]

For the record: the force needed for the circle trajectory is 4mg towards the centre. 4g is an acceleration. And yes, the acceleration towards the centre of a circular trajectory is v²/r

While going straight down at constant speed, the pilot experiences 1g downward. This is a vector.
As soon as he pulls the wheel (or what do they call it) towards him, a uniform circular motion sets in that requires 4g of acceleration towards the centre. His seat provides the force required for that acceleration. Also a vector, initially pointing to the right. So initially he feels an acceleration of 1 g down, 4g to the right. √17 magnitude total. Gradually going towards 1 g down and 4 g down as well just before point q. Magnitude now 5 g (same direction). He can stand that as per given in the OP. If he's smart he pulls up a little longer, haha. The moment he is going straight again, he experiences 1 g towards the center of the earth.

I can follow your reasoning in this post. But two questions. In moving vertically down(just before making the pull up), why is there a 4g acceleration towards the center? Wouldn't it make more sense to say that there exists a 4g acceleration to the center at the instantaneous moment when the "pull-up" was made?

Gradually going towards 1 g down and 4 g down as well just before point q. Magnitude now 5 g (same direction). He can stand that as per given in the OP. If he's smart he pulls up a little longer, haha. The moment he is going straight again, he experiences 1 g towards the center of the earth.

If the pilot is along the arc length conjoining (-r,0) and (0,-r), How is the magnitude now 5g? Can you demonstrate the mathematical reasoning behind how 5g is achieved? (4g+1g?) The pilot experiences 1g towards the center of the Earth and 4g to the center of the circular path, isn't it? Wouldn't that be a SQRT(17) as you have aforementioned?

 

[rcgldr]

The pilot experiences 1g towards the center of the Earth and 4g to the center of the circular path, isn't it? Wouldn't that be a SQRT(17) as you have aforementioned?

What the pilot experiences is how hard the seat is pushing the pilot "upwards". At the bottom of the climb out, the seat is generating 4 m g of centripetal force and 1 m g of force opposing gravity.

 

[negation]

What the pilot experiences is how hard the seat is pushing the pilot "upwards". At the bottom of the climb out, the seat is generating 4 m g of centripetal force and 1 m g of force opposing gravity.

What's the variable, 'm', by the way?

Edit: I see, mass. mg = w

 

[negation]

What the pilot experiences is how hard the seat is pushing the pilot "upwards". At the bottom of the climb out, the seat is generating 4 m g of centripetal force and 1 m g of force opposing gravity.

EDIT: So in totality, the pilot experiences only net 3g acceleration? At point q(0,-r), there is a 4g acceleration up and 1g acceleration down.

 

[negation]

SQRT(24g^2) = 48ms^-2

g = v^2/r

r = 2310m