Help Me Solve My Diagram Problem: Calculating Center of Mass

[jisbon]

Homework Statement

Two identical uniform triangular metal played held together by light rods. Caluclate the x coordinate of centre of mass of the two mass object. Give that mass per unit area of plate is 1.4g/cm square and total mass = 25.2g

Relevant Equations

-

Not sure what I went wrong here, anyone can help me out on this? Thanks.
EDIT: Reformatted my request.
Diagram:

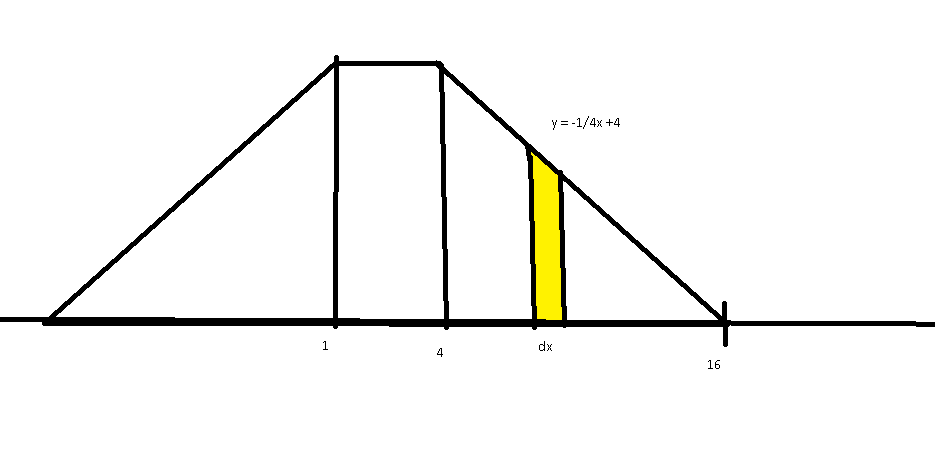
So as far as I know to calculate the center of mass for x, I have to use the following equation:
COM(x):
$\frac{1}{M}\int x dm$
And I also figured that to find center of mass, I will have to sum the mass of the 2 plates by 'cutting' them into stripes, giving me the following formula:
$dm = \mu * dx * y$ where $\mu$ is the mass per unit area.
So subbing in the above equation into the first, I get:
$\frac{1}{M}\int x (\mu * dx *y)$
$\frac{\mu}{M}\int xy dx$
Since the 2 triangles are identical, I can assume triangle on the left has equation $y = 1/4x +4$
This is the part where I'm not sure. Do I calculate each of the triangle's center of moment, sum them and divide by 2? Or am I suppose to use another method?
Regardless of what, supposed I am correct:

COM for right triangle:
$\frac{\mu}{M}\int_{4}^{16}x(\frac{1}{4}x+4) dx$ = 8 (expected)

COM for left triangle:
$\frac{\mu}{M}\int_{-11}^{1}x(-\frac{1}{4}x+4) dx$ = 5.63...

Total COM = $8+5.63/2$ which is wrong :(

Thanks

 

[mfb]

Your equations are hard to read (writing them here would help) and you don't explain what you do either.
If the x-axis is horizontally why don't you just use the symmetry of the problem?

 

[Delta2]

If the mass density of the two triangles is uniform, then there is a pure geometric method to find the center of mass, that depends only on the shape of the triangles. But I am not sure whether you are allowed to use this method. Anyway for uniform mass density the center of mass is the so called centroid or barycenter of the triangle, which is the point that the three medians of the triangle intersect.

 

[jisbon]

Your equations are hard to read (writing them here would help) and you don't explain what you do either.
If the x-axis is horizontally why don't you just use the symmetry of the problem?

If the mass density of the two triangles is uniform, then there is a pure geometric method to find the center of mass, that depends only on the shape of the triangles. But I am not sure whether you are allowed to use this method. Anyway for uniform mass density the center of mass is the so called centroid or barycenter of the triangle, which is the point that the three medians of the triangle intersect.

Updated my question :)

 

[Delta2]

Certainly there is something wrong with that 5.63... Do the integral again.
and I believe the integral must be $$\int_{-11}^{1}x(x/4+\frac{11}{4})dx$$

 

[jisbon]

Certainly there is something wrong with that 5.63... Do the integral again.
and I believe the integral must be $$\int_{-11}^{1}x(x/4+\frac{11}{4})dx$$

Realized I used the wrong equation, answer turns out to be -7.16666...
It's still wrong though :/

 

[Delta2]

Use the integral I posted at post #5 the correct y(x) for the left triangle is $y=\frac{x+11}{4}$. You ll find the x-coordinate for the center of mass of the left triangle to be -3.

 

[jisbon]

Use the integral I posted at post #5 the correct y(x) for the left triangle is $y=\frac{x+11}{4}$. You ll find the x-coordinate for the center of mass of the left triangle to be -3.

Oh yes the y intercept :/ I 'think' too much about identical, even the intercepts :/ Thanks tho :) Answer is 2.5 :)

 

[mfb]

Answer is 2.5

Right.
Note that 2.5 is exactly the middle between the two triangles. The setup is symmetric, it can't be anywhere else. Finding symmetries like this can often save lengthy calculations.