Jamister
- 58
- 4
In balanced homodyne detection, it is claimed that one can do state tomography. I understand most of the derivation except one part. Here is a figure describing homodyne detection.
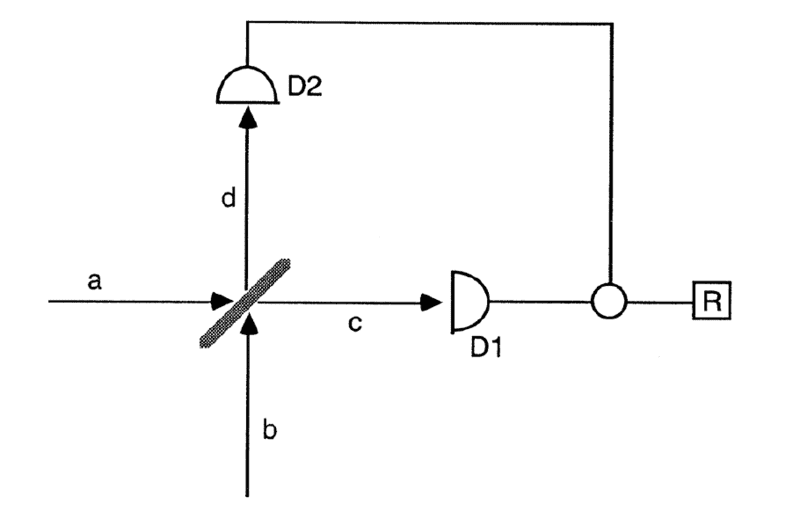
the operator that is being measured is
$$ R=N_{1}-N_{2}=a^{\dagger} b+b^{\dagger} a $$.
taking the mode b to be coherent state, we obtain:
$$R=r\left(a^{\dagger} e^{i \phi}+a e^{-i \phi}\right)=\sqrt{2} r q_{\phi}$$.
Now what I don't understand is that what is being measured is discrete photon counts. On the other hand, the spectrum of the operator ##q_{\phi}## is continuous. Therefore, how can obtain ##\langle q_{\phi} \vert \rho \vert q_{\phi} \rangle ## from the measurements?
the operator that is being measured is
$$ R=N_{1}-N_{2}=a^{\dagger} b+b^{\dagger} a $$.
taking the mode b to be coherent state, we obtain:
$$R=r\left(a^{\dagger} e^{i \phi}+a e^{-i \phi}\right)=\sqrt{2} r q_{\phi}$$.
Now what I don't understand is that what is being measured is discrete photon counts. On the other hand, the spectrum of the operator ##q_{\phi}## is continuous. Therefore, how can obtain ##\langle q_{\phi} \vert \rho \vert q_{\phi} \rangle ## from the measurements?