bardia sepehrnia
- 28
- 4
- TL;DR
- Thermodynamics, entropy and reversibility
In the book for our thermodynamics, it states that a process that is internally reversible and adiabatic, has to be isentropic, but an isentropic process doesn't have to be reversible and adiabatic. I don't really understand this. I always thought isentropic and reversible mean the same thing, process that leads to no entropy generation should be by definition, reversible?
The book also keeps mentioning the word "internally" reversible which I don't understand what it means despite reading about it from 100 different sources.
So can anyone give me an example of:
1- An isentropic process that is not reversible not adiabatic? (no entropy generated, yet heat is transferred?)
2- A reversible process that is "not" adiabatic and "not" isentropic? (A graph in the book demonstrate that a process can be reversible, despite heat transfer)
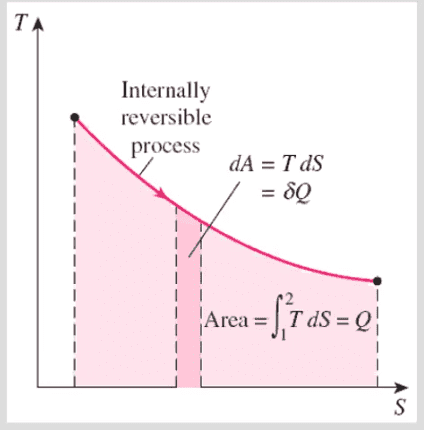
The book also keeps mentioning the word "internally" reversible which I don't understand what it means despite reading about it from 100 different sources.
So can anyone give me an example of:
1- An isentropic process that is not reversible not adiabatic? (no entropy generated, yet heat is transferred?)
2- A reversible process that is "not" adiabatic and "not" isentropic? (A graph in the book demonstrate that a process can be reversible, despite heat transfer)
