How can I calculate the time for non-uniform acceleration in a circular path?

[Cato11]

TL;DR Summary

How to achieve non-uniform acceleration?

Hello everyone, I would really appreciate some help with a challenge I am facing. The challenge is to accelerate a particle in a circular path, but the acceleration must be non-uniform. In other words, the velocity does not increase linearly. The problem I am facing is shown below:

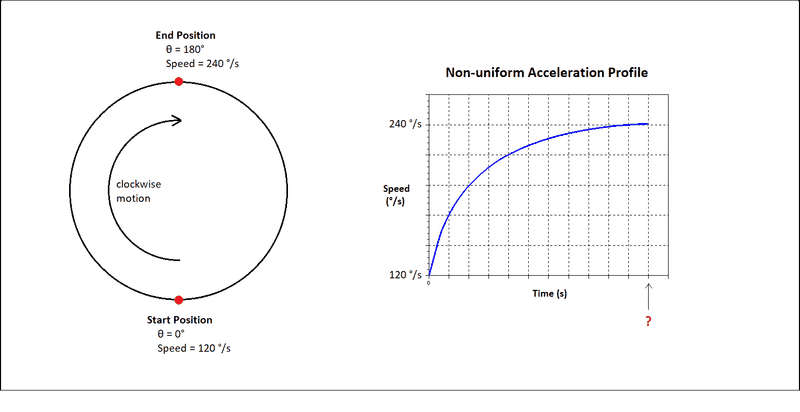
The scenario:
1. The particle starts at the Start Position (in this case 0°) with a speed of 120°/s.
2. The particle must accelerate to the End Position (in this case 180° away) where it has a speed of 240°/s
3. The acceleration must follow the profile in the graph, i.e. it must accelerate rapidly at the start after which the rate should decrease

The problem:
- Does anyone know how I can find the time (t) it takes to undergo this acceleration? It must occur precisely within the 180° of displacement.

The context:
I am writing a computer program to animate this motion. I can quite easily alter the particle's speed to follow the curve, but I need to know the timescale within which to do this. As a side note, I have been able to achieve uniform acceleration in this scenario using the rotational versions of the linear motion equations, but I believe that these no longer apply in the case of non-uniform acceleration. Please correct me if I am wrong though.

Any help would be appreciated tremendously!

 

[PeroK]

You need to define the acceleration function in your graph.

 

[Cato11]

You need to define the acceleration function in your graph.

Please can you advise how to go about this?

 

[PeroK]

Please can you advise how to go about this?

Either you have a function in mind; or, you do a numerical estimate of the graph you have drawn.

Note that at a starting rotation of 120 degrees per second, it's only going to take $1.5s$ to rotate by 180 degrees. With the acceleration, the total time will be less a second, at a rough estimate.

Mathematically, the area under the graph you have drawn must be $180$ units (degrees). You need to adjust the scale on the time axis so that this is true. As above, that means that $t \approx 1s$.

A quick way to do this is to calculate the average rotational speed - either by integrating your chosen function or using the graph. You would get the total time from that.

 

[Cato11]

Either you have a function in mind; or, you do a numerical estimate of the graph you have drawn.

Note that at a starting rotation of 120 degrees per second, it's only going to take $1.5s$ to rotate by 180 degrees. With the acceleration, the total time will be less a second, at a rough estimate.

Mathematically, the area under the graph you have drawn must be $180$ units (degrees). You need to adjust the scale on the time axis so that this is true. As above, that means that $t \approx 1s$.

A quick way to do this is to calculate the average rotational speed - either by integrating your chosen function or using the graph. You would get the total time from that.

Thank you PeroK, I understand the gist of what you are saying but I am not sure how to implement your recommendations. Could you possibly provide a worked example of your solution? I have tried looking at worked examples online but they always involve a known timeframe, so I am just perplexed as to how to define these functions you are mentioning.

A worked example would be really appreciated to help me understand the steps and the math.

 

[PeroK]

If you look at your graph, you have unknown units of time ($\Delta t$)along the horizontal axis, and units of 24 degrees/s on the vertical axis . During the first unit of time the rotational speed increases from 120 to 168 degrees/s. The simplest approach is to take the average of 144 degrees/s as the average rotation duing that time unit. That means the object moved through an angle of $144 \Delta t$ degrees.

During the second time unit, the speed increased from 168 to 192 degree/s. Again taking the average gives a further rotation of $180 \Delta t$.

If you do that for all time intervals, you get the equation for the total rotation, which must be 180 degrees:
$$180 = (144 + 180 + 200 + 212 + \dots + 240)\Delta t$$
That gives you an estimate for $\Delta t$ in seconds.

Clearly you can only do this with a precision related to how well you know the precise acceleration profile in your diagram. I'm just reading off the values as I can see them.

 

[Cato11]

But doesn't this mean that deltaT just becomes smaller the more intervals we compute? E.g. if I am very precise and compute 1000 intervals, I will get a much smaller deltaT than if I did 10 intervals. This would produce a massively different timeframe depending on how accurate I am, but surely this should not be the case? I am assuming the red question mark in my image becomes equal to the deltaT I find.

I am probably being very dim here!

 

[PeroK]

But doesn't this mean that deltaT just becomes smaller the more intervals we compute? E.g. if I am very precise and compute 1000 intervals, I will get a much smaller deltaT than if I did 10 intervals. This would produce a massively different timeframe depending on how accurate I am. I am assuming the red question mark in my image becomes equal to the deltaT I find.

I am probably being very dim here!

Once you have $\Delta t$ you have to multiply it by the number of units on the graph!

 

[Cato11]

Once you have $\Delta t$ you have to multiply it by the number of units on the graph!

D'oh!

I think that has fixed it.. not sure how I made such a ridiculous oversight!

 

[Cato11]

Okay so I have just run some code using this method and on first impressions it seems to have produced exactly the correct result! Seriously I cannot thank you enough PeroK!

I still have to implement this in many different scenarios so if I run into an issue I will let you know, but for now it seems to have solved my problem. I appreciate your help tremendously!

 

[kuruman]

For whatever it's worth but mostly to satisfy my own curiosity, I investigated what kind of functions might do the required job. I came up with an angular speed given by $$\omega(t)=\omega_0\left(1+\frac{5t}{1+4t^{4/3}}\right).$$Here, $\omega_0=120~\text{deg/s}$. The integral of the equation above is, $$\theta(t)=\omega_0\left[t+\frac{15}{8}t^{2/3}-\frac{15}{16}\arctan\left(2t^{2/3}\right)\right].$$ The equations predict that at final time $t_{\!f}=0.832~\text{s}$, the angle is 180.0° and the angular speed 240.9 deg/s. The two equations are plotted below.

 

[Cato11]

Once you have $\Delta t$ you have to multiply it by the number of units on the graph!

Hi PeroK,

Can I please ask if your method works for any shaped path? In the case of this thread, the particle moves in an arc (or circular) path. But let's say it instead moved in a different shape, say a 'U' shape or any other shape, does the same math still apply? Obviously total distance of 180° would change to the length of the new path, but aside from that can we use the same method?

Cheers,
Cato

 

[kuruman]

Hi PeroK,

Can I please ask if your method works for any shaped path? In the case of this thread, the particle moves in an arc (or circular) path. But let's say it instead moved in a different shape, say a 'U' shape or any other shape, does the same math still apply? Obviously total distance of 180° would change to the length of the new path, but aside from that can we use the same method?

Cheers,
Cato

A "U" turn should be easy. You can add as much constant velocity motion (zero acceleration) at the beginning and end of the path to what you already have, and then rescale the time uniformly if you need to. "A different shape" might be easy or difficult depending on the specifics of the shape. In principle, you can simulate any path with straight pieces and turns by varying angles, not necessarily 180° each. In my opinion, the task would be easier if you had an expression for the velocity as a function of time.

 

[Cato11]

Thanks Kuruman. So I have tried using this method for a range of differently shaped paths, e.g. an S shaped path, random wiggly lines etc. I believe the method works for any scenario, so long as the length of the path is known.

The method I am describing is effectively PeroK's graph method:

1. Calculate the time 't' of the acceleration by finding the area under the Velocity-Time graph, and dividing the path length by this (can be metres, degrees etc.)
2. Plot a scaled Velocity-Time graph where the real 't' is on the x-axis
3. Plot a Displacement-Time graph using step integrals on the Velocity-Time graph
4. Use the Displacement-Time graph to drive progress along the path:
   1. Calculate a ratio of progress along the path using the Displacement-Time graph, e.g. if mid-way through the acceleration time it is 2m along a 5m path, then ratio = 0.4
   2. Define a function that maps all positions along the path between 0 and 1, i.e. P(0) is the start and P(1) is the end of the path
   3. Feed the ratio into that function as time progresses

From what I can tell, this accelerates a particle along different shaped paths using any acceleration profile. It is incredibly useful. The function in Step 4.2. is a challenge of its own, but there are many Bezier Curve libraries that provide such a function, enabling you to draw any shaped path you want and return a position as a function of time (between 0 and 1).