How can I find t in a Bezier Curve when I know the Y coordinate?

[Gabor888]

Hello

I have a little problem with bezier curve. There is a bezier curve, with n degree, with some control points. And the problem is, that i want to know the t, and i know the y of that point. So there's a curve, in this curve there is a point, i know that place, and i want to know, what is t in this bezier.

With this algorithm(which i attached) i know the point, if i know the t

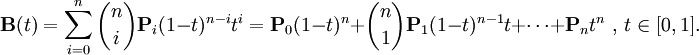
but reverse?

i know, that the t can be more numbers. I want just one of them...

 

[dodo]

The Y(t) coordinate of the 2-dimensional B(t) equation you posted is a polynomial of degree n; what you want are the solutions of the equation Y(t) - Ygiven = 0, that is, the roots of the polynomial Y(t) - Ygiven, where Ygiven is your known Y value. The expression for Y(t) is, of course, the same as in the image you posted, substituting each point P with the Y value of that point. Among the multiple values for t, you want the one(s) that are in the interval [0,1].

If n is small (like 2) there are known methods. Otherwise, a possibility is to use an iterative method like Newton's, since the derivative of the polynomial should be easy to write down. See, for example, http://en.wikipedia.org/wiki/Newton%27s_method" . Or maybe the polynomial turns out to be easy to factor, in which case the roots can be taken immediately from the factored expression.