Mech_LS24
- 148
- 16
- TL;DR Summary
- I would like to solve the equation for "d".
Dear mathematicians,
I am getting stuck solving this equation for "d". And what (free)software would you recommend to check this equation?
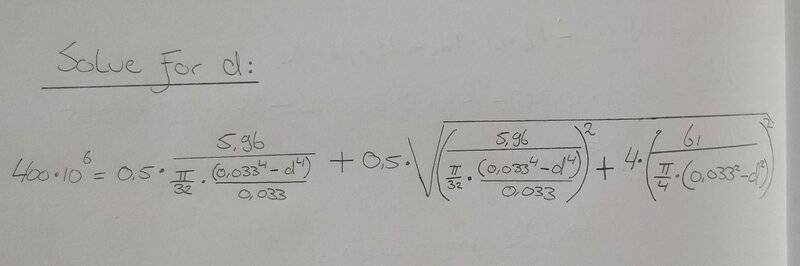

Thanks a lot!
I am getting stuck solving this equation for "d". And what (free)software would you recommend to check this equation?
Thanks a lot!