Ted Farkas
- 19
- 0
Hi
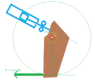
This is a simplified force diagram of a problem I have of some machinery. (shown in same thread)
I am trying to get the output force a
My calcs gave me 1.5 ton for A and 612 kg for B diagram.
when the leverage is not a straight seesaw - do you take arm length from pivot or is one arm taken as perpendicular height.
Also the force is a ram, do you need to workout a resultant force with the x and y-axis or can you just assume 5.1 ton is acting on the pivot arm.
I hope this makes sense.
I am working through my old engineering text but everything is a nice easy 'see saw' diagram
thanks
Ted
This is a simplified force diagram of a problem I have of some machinery. (shown in same thread)
I am trying to get the output force a
My calcs gave me 1.5 ton for A and 612 kg for B diagram.
when the leverage is not a straight seesaw - do you take arm length from pivot or is one arm taken as perpendicular height.
Also the force is a ram, do you need to workout a resultant force with the x and y-axis or can you just assume 5.1 ton is acting on the pivot arm.
I hope this makes sense.
I am working through my old engineering text but everything is a nice easy 'see saw' diagram
thanks
Ted