albertseng
- 2
- 0
Hello,
Uncle have one question.
How to calculate the deflection of the upper flange if the pipe configuration is like the attached picture. How to include the weight of the pipe, can I assume it as the distribution load? And what if there is another load acting downward at the middle of the upper side.
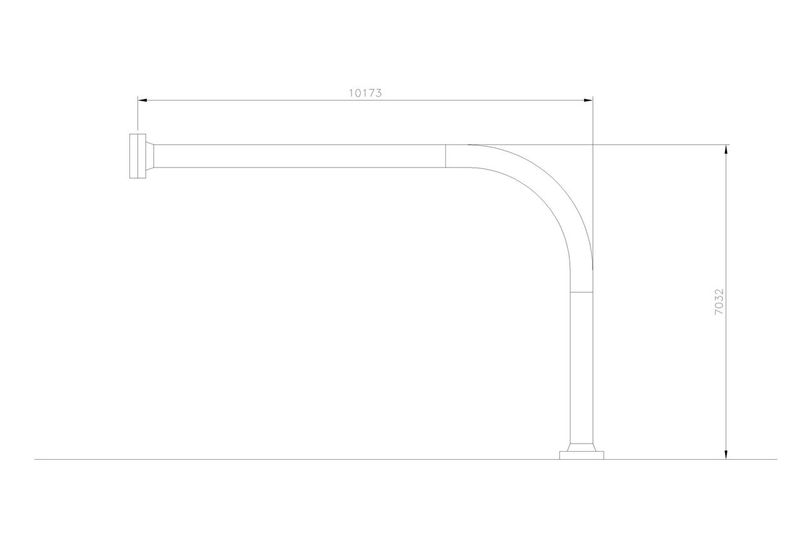
Uncle have one question.
How to calculate the deflection of the upper flange if the pipe configuration is like the attached picture. How to include the weight of the pipe, can I assume it as the distribution load? And what if there is another load acting downward at the middle of the upper side.