How do you solve for g(x) using given points on the graph of f(x)?

[Peter G.]

Hi,

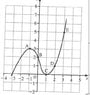
The sketch (attachment) shows part of the graph of y = f (x) which passes through the points:

A (-1,3) B (0,2), C (1,0), D(2,1) and E (3,5)

A second function is defined by g (x) = 2f (x-1)

a) Calculate g (0), g(1), g(2) and g (3)

I am confused about what the question is asking... Could anyone maybe give me a clue/guide with one of the points so I can try and do the rest on my own?

Thanks,
Peter G.

 

[danago]

Think about how g(x) is related to f(x).

eg. g(0) = 2f(-1)

You could use the graph to find f(-1)

 

[Peter G.]

so, when g (0), we sub x for 0, giving us: 2f(0-1) = 2f(-1)

Then, I can go to the graph, find the value for y when x = -1 and multiply by 2?

 

[danago]

Yep. You could also think about it in terms of transformations; the graph of g(x) is just the graph of f(x) that has been shifted to the right by 1 unit and then stretched parallel to the y-axis by a factor of 2. This means that the point with coordinate (-1,3) becomes (0,6).

 

[Peter G.]

Yeah, that was what I thought about first but I am a bit sleepy and for some reason couldn't do it

Thanks a lot,
Peter G.