How Does Angular Velocity Affect Instantaneous Acceleration in Rotating Systems?

[WMDhamnekar]

Homework Statement:: Find the instantaneous acceleration of a projectile fired along a line of longitude (with angular velocity of $\gamma$constant relative to the sphere) if the sphere
is rotating with angular velocity $\omega$.
Relevant Equations:: None

Find the instantaneous acceleration of a projectile fired along a line of longitude (with angular velocity of $\gamma$ constant relative to the sphere) if the sphere is rotating with angular velocity $\omega$. Using the following author's answer, I computed instantaneous acceleration of a projectile fired $\ddot{r}= -\gamma^2 r + 2\omega \gamma r \cos{\gamma t } \hat{\ell} -\omega^2 r \sin{\gamma t}\hat{n}$

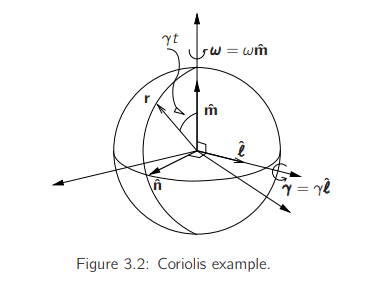
Now, what is the instantaneous acceleration in case of Rocket instead of Projectile?

I don't understand the author's explanation which is as follows:

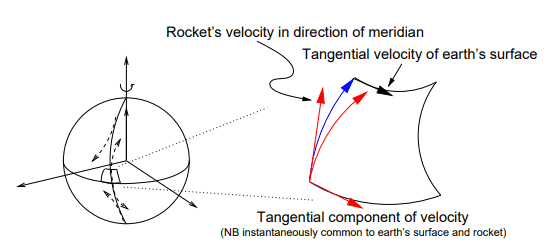
Would anyone here explain me the exact meaning of author's explanation and above picture?[Moderator's note: moved from a homework forum.]

 

[jbriggs444]

I disagree with the author's description.

The author is describing a "reactive Coriolis force" -- the real force required to resist the inertial Coriolis force which manifests in the rotating frame.

The Coriolis force is the eastward inertial force which would cause a deflection away from the rails.

This Coriolis force is an inertial force. It exists in the rotating frame only. In other frames, the same accelerating separation from the rails would still exist (were it not for the force from the rails). But that separation would be explained differently. For instance, in an inertial frame, we would have a straight line trajectory deviating from a curved and accelerating set of rails below it.

The "reactive Coriolis force" is the westward interaction force from the rails which keeps the object on the rails in spite of this.

Some adjectives for "real" forces: Interaction, real, physical, reactive
Some adjectives for "fictitious" forces: Inertial, fictitious, pseudo

"Interaction" and "inertial" are nice adjectives because they are descriptive and not pejorative.

Edit to add...

The adjective "reactive" is one that I've never seen applied to the Coriolis force. It is commonly used when talking about the centrifugal force. I use it here in a somewhat analogous way:

The inertial centrifugal force is the fictitious force that manifests in a rotating frame and explains the tendency of a ball on a string to fly away from the center.

The "reactive" centrifugal force is the real force from the ball on the string that holds the ball on its circular path in spite of its tendency to fly away.