How Does Archimedes' Estimation of Pi Hold for n=4, 8, 16, 32, ...?

[nacho-man]

It has been eons since I've done any trigonometry, but I just can't prove how this following relationship holds for $n = 4, 8, 16, 32, \dots$

The relation is:
$$
2 \biggl( \! \frac{A_{2n}}{n} \! \biggr)^2 = \, 1 - \Biggl( \sqrt{1 - \frac{2A_n^{\phantom{X}}}{n}} \, \Biggr)^{\!2}
$$

I've subbed in points, and it definitely holds.

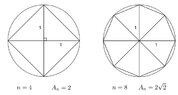
Using this image as reference, a polygon with $n$ edges and $A_n$ the entire area, we can estimate (albeit very slowly) a unit circle's area.View attachment 4126Any help would be appreciated.

 

[Nono713]

In your equation the right-hand-side takes a square root and then immediately squares the result, what does that amount to? Once you've simplified your equation using that fact, think about what $A_n / n$ and $A_{2n} / n$ represent geometrically, and you can then perhaps reduce the algebra problem to a geometric statement about triangles.

 

[nacho-man]

In your equation the right-hand-side takes a square root and then immediately squares the result, what does that amount to? Once you've simplified your equation using that fact, think about what $A_n / n$ and $A_{2n} / n$ represent geometrically, and you can then perhaps reduce the algebra problem to a geometric statement about triangles.

I have solved this problem now.

Thanks :)

 

[Nono713]

I have solved this problem now.

Thanks :)

Great! It's good etiquette to post your solution so that future visitors who come across this thread can also benefit from it :)

 

[nacho-man]

Great! It's good etiquette to post your solution so that future visitors who come across this thread can also benefit from it :)

Yes! definitely.

I will post the solution some time next week, when my work has been assessed (don't want to post a solution with errors and mislead someone :( )