How Does Energy Conservation Affect SHM in a Mass-Spring System?

[gnits]

Homework Statement

Analysis of SHM of a mass

Relevant Equations

F=ma

Could I please ask for views on this question:

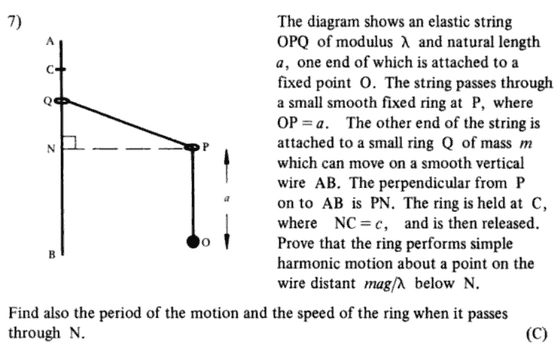
I've answered the whole thing and agree with the answers given in the textbook.

Here are those answers (where Y is the modulus of elasticity of the string = lamda in the question):

Period of motion = 2 * PI * sqrt( ma/Y )

Speed passing through N = sqrt( 2gc + Yc^2/ma )

In answering the last part I made use of conservation of energy as follows:

let D = distance from N to lowest point reached by ring.
Let L = |PN|
Let zero potential energy be at the level of O then:

Energy at C = energy at Lowest point so:

Potential Energy of mass at highest point + elastic energy at highest point = elastic energy at lowest point

so, using energy in elastic string = Yx^2/2a where x = extention and a = natural length gives:

Y(L^2 + c^2) / (2a) + mg(c+D) = Y(L^2 + D^2) / (2a)

and this leads to two values for D:

D = -c

and

D = (2agm/Y) + c

Which one is the correct one and why?

The first one seems to imply that the mass will go down to a position eqally distant below the level of O as it was above the level of O and so as energy is not lost in the system, would this not give an oscillation about the point N? (rather then the answer of a point mag/Y below N)

The second solution would imply a depth greater then that which it started out above N by an amount 2agm/Y.

Thanks for any help in clarifying,
Mitch.

 

[Cutter Ketch]

Homework Statement: Analysis of SHM of a mass
Homework Equations: F=ma

Y(L^2 + c^2) / (2a) + mg(c+D) = Y(L^2 + D^2) / (2a)

The way you wrote this equation D is positive in the downward direction and is measured from N. Also, having no gravitational potential energy on the right side this is also explicitly at the bottom. Therefore D = -c is not meaningful. Among other things it would mean you started with no potential energy on the left. You ignored the sign of D when you analyzed that both answers were down below N. At D = c (down below N, right?) the elastic energy is the same as the start but the gravitational energy has been reduced. It makes sense that the ring must continue past c down until the elastic energy grows to be equal to the original elastic energy PLUS the lost gravitational potential energy. So D is and should be greater than c.

What happened here is that you wrote a correct relation between scalar quantities but the coordinates and signs (and missing terms) were all predetermined by construction. You then forgot the hidden assumptions in the construction. You would have been better off explicitly parameterizing the motion in a coordinate system (as it seemed you were about to do when you said O = zero potential) keeping consistent signs as demanded by the coordinate system and keeping all factors on both sides of the equation. Then substitute positions with the proper signs. This way all confusion about signs, positions, and meanings are avoided.

 

[gnits]

Thanks very much for your reply, your explanation makes perfect sense. I've learned from that.
Mitch.