Albert1
- 1,221
- 0
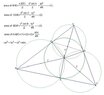
Point $I$ is the incenter of $\triangle ABC $
giving :$BC=a , \, AC=b,\, AB=c$
$IA=x, \, IB=y, \, IC=z$
prove :$ax^2+by^2+cz^2=abc$
giving :$BC=a , \, AC=b,\, AB=c$
$IA=x, \, IB=y, \, IC=z$
prove :$ax^2+by^2+cz^2=abc$