How does the pressure drop as a fluid flows through a pipe

[jbriggs444]

I think the OP is trying to apply rules appropriate to the static situation (no flow, pressure is equal throughout the pipe) to the dynamic situation, where the fluid is in motion. There's nothing "common sense" about the latter, at least not when it comes to the math.
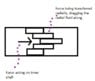
Imagine 20 psi at one end of a mile-long 1-inch pipe, and explaining "what happened" to the pressure at the far end, where the water is barely dripping out. Close off the far end, though, and the pressure jumps instantly to 20 psi. Chestermiller can explain it, but it's baffling to the amatuers in the room.

If you close off the far end, the pressure at the near end does not jump to 20 psi. It was already at 20 psi. If you close off the far end, the pressure at the far end does not jump instantly to 20 psi. It jumps instantly to an extreme value and the pipe may break.

It is only after the system has settled down into a new equilibrium after some seconds (speed of sound in water is in the neighborhood of one mile per second) that it attains a condition of 20 psi throughout.

Which, I suppose, makes your point about the details not being intuitively obvious.

 

[zul8tr]

From original post:
"Where it becomes abstract for me is following a section of this fluid as it travel along the pipe and what happens to it
(A) I think it experiences a net force of 0 at all points because it is not accelerating. I am assuming the opposing force due to friction is keeping the net force at 0.
(B) I am having trouble understanding why pressure gradually drops along the pipe or hose. The rightward pointing force acting on it is getting reduced. How exactly does this happen? If the fluid is incompressible, why isn't this section still feeling the same force as it did as the initial point in the hose?
-----------------------------------------------------------------
(A) for steady state in equilibrium the net force is zero but a net hydraulic gradient per unit length is developed and that results in the unit driving force
(B) The hydraulic gradient drops in the flow direction to maintain the driving force to move the fluid along, if the flow is reduced to zero then the pressure driving force = 0.

A bit more detail:
In steady state (dv/dt partial = 0) incompressible flow all forces are in balance and if the pipe diameter is assumed constant then no convective acceleration (v dv/dx partial = 0) exists since mean velocity is constant and a hydrostatic pressure distribution (straight and parallel streamlines) exists at any cross section. Then in this case a linear hydraulic gradient is established that always drops in the flow direction. This hydraulic gradient has a constant unit pressure drop along the pipe or a unit pressure difference and that here is the constant unit driving force developed on each cross section area all along the pipe, that is exactly balanced by the unit fluid friction force (no gravity force if the pipe is horizontal). The hydraulic gradient is a function of the total system geometry, fluid type, etc and the beginning and end points (boundary conditions) that establishes the total system mass flow achieved.

There is no energy lost it is just converted to other forms and not recoverable in this irreversible process resulting from friction.

Above discussion a small diameter pipe was considered with pressure measured at the center of the pipe, but if the pipe diameter is large and with a hydrostatic pressure distribution at any cross section then there is a pressure difference from the top to the bottom of the pipe (say horizontal pipe for this discussion) and that internal transverse force is transferred into the pipe wall as stresses and strains.This does not generally change the unit pressure driving force in the pipe length direction. In any pipe flowing with say a Newtonian fluid the velocity varies from zero at the pipe wall (stick condition) to generally max velocity at the pipe center with a transverse velocity distribution depending on the state of flow: with laminar flow it is parabolic and logarithmic for full turbulent flow. Other type very different fluids can have very different velocity distributions but the stick condition at the wall is always present.

In the CV system with flexible walled arteries down to super small capillaries then back to veins and to the heart pumping away the hydraulic process is the same but much more complected with variable hydraulic gradients in variable pulsing flow conduit diameters responding to the pulsing pressure changes by the heart.

 

[seratia]

What exactly does pressure loss due to friction mean? How do you even visualize that?

 

[jbriggs444]

What exactly does pressure loss due to friction mean? How do you even visualize that?

Can you visualize the tension of a fuzzy rope drawn through a slightly tight tube?

 

[seratia]

Can you visualize the tension of a fuzzy rope drawn through a slightly tight tube?

I can. But that doesn't mean I can relate it to pressure drop.

And also: Why can't a constant pressure drive the fluid through the pipe? Why does it have to decrease for there to exist a flow. When I drag a book across the floor at constant speed, I do so with constant pressure. Why must there be a pressure loss in order for the fluid to flow?

 

[Chestermiller]

I can. But that doesn't mean I can relate it to pressure drop.

And also: Why can't a constant pressure drive the fluid through the pipe? Why does it have to decrease for there to exist a flow. When I drag a book across the floor at constant speed, I do so with constant pressure. Why must there be a pressure loss in order for the fluid to flow?

When you push a book across the floor at constant speed, the force you are exerting on the back end of the book is higher than the (no) force you are exerting on the leading end of the book. So there actually is a pressure loss.

To get an idea of viscous friction, think extreme cases like very viscous fluids like molasses, pancake syrup, and corn syrup. Imagine that you have the fluid contained between two horizontal parallel plates, and you are trying to slide the top plate to the right at constant speed. You need to exert a force on the upper plate to the right and a force on the lower plate to the left to hold it in place. OK so far?

 

[seratia]

When you push a book across the floor at constant speed, the force you are exerting on the back end of the book is higher than the (no) force you are exerting on the leading end of the book. So there actually is a pressure loss.

That makes sense. Someone else in this thread also told me something like this actually, which I forgot about. This is the best example so far. So the middle of the book has half the pressure?

I think I understand - so the fluids pressure stays proportional to how much fluid it has in front of it?! If so, that makes total sense! But I wouldn't call that "loss due to friction".

To get an idea of viscous friction, think extreme cases like very viscous fluids like molasses, pancake syrup, and corn syrup. Imagine that you have the fluid contained between two horizontal parallel plates, and you are trying to slide the top plate to the right at constant speed. You need to exert a force on the upper plate to the right and a force on the lower plate to the left to hold it in place. OK so far?

When you say "hold it in place", what do you mean?

 

[Chestermiller]

That makes sense. Someone else in this thread also told me something like this actually, which I forgot about. This is the best example so far. So the middle of the book has half the pressure?

Yes.

I think I understand - so the fluids pressure stays proportional to how much fluid it has in front of it?! If so, that makes total sense!

Only if the exit is at zero pressure. What you really want to look at the the difference in pressure between two locations along the pipe axis; like your example of full pressure at the back, and half the pressure at the middle. This is proportional to the "frictional" force at the pipe wall acting on the fluid between the two locations.

But I wouldn't call that "loss due to friction".

But that is exactly what it is: loss in pressure between two locations due to viscous friction at the wall.

When you say "hold it in place", what do you mean?

Don't allow it to move.

 

[seratia]

But that is exactly what it is: loss in pressure between two locations due to viscous friction at the wall.

It seems to me that you are viewing force as some kind of momentum, reducing as it encounters friction along its journey.

Don't allow it to move.

Like this?

 

[Chestermiller]

It seems to me that you are viewing force as some kind of momentum, reducing as it encounters friction along its journey.

This makes no sense to me. A force is just a force.

Like this?

View attachment 235814

This makes no sense to me either.

 

[Chestermiller]

Have you had a course in introductory physics that includes forces and free body diagrams?

 

[BvU]

It seems to me that you are viewing force as some kind of momentum

Force is the time derivative of momentum. Momentum is transported sideways by viscosity. (Did I say something like that before?)

 

[seratia]

This makes no sense to me either.

I mean, that's what your description was, lol

 

[seratia]

Force is the time derivative of momentum. Momentum is transported sideways by viscosity. (Did I say something like that before?)

To say that momentum is transported sideways is to imply that the force is acting at the center of the fluid, and the radial fluid is carried along by shear stress (thus momentum). When I asked before if the force is acting on the middle, I was told no, it acts against the cross sectional area all at once.

Is this what you mean:

 

[seratia]

Have you had a course in introductory physics that includes forces and free body diagrams?

Yes.

As it applies to this problem, the force pushing the fluid against friction (pushing the fluid from left to right) is getting reduced (I am assuming because of the friction it has incurred to get from the beginning of the journey to the middle of the journey, if for example we look at those two points).

 

[Chestermiller]

I mean, that's what your description was, lol

Please point out where I said anything about momentum.

 

[seratia]

Have you had a course in introductory physics that includes forces and free body diagrams?

This is not a free body diagram. But it gets the point across:

As you can see, force is lessened at point 2.

 

[seratia]

Please point out where I said anything about momentum.

Not about momentum. But about the description of the two plates. Here is what you said:

"To get an idea of viscous friction, think extreme cases like very viscous fluids like molasses, pancake syrup, and corn syrup. Imagine that you have the fluid contained between two horizontal parallel plates, and you are trying to slide the top plate to the right at constant speed. You need to exert a force on the upper plate to the right and a force on the lower plate to the left to hold it in place. OK so far?"

This is how I interpreted it:

It seems you are wanting to oppose the fluid moving with the plates - so "holding it in place" as you said ("it" being the fluid) while you move the plates, the upper plate to the right and the lower plate to the left.

 

[Chestermiller]

Yes.

As it applies to this problem, the force pushing the fluid against friction (pushing the fluid from left to right) is getting reduced (I am assuming because of the friction it has incurred to get from the beginning of the journey to the middle of the journey, if for example we look at those two points).

Since you have had a course in freshman physics, I have a focus problem for us to work on. Consider two parallel plates with viscous fluid situated between them. One plate is at z = 0 and the other plate is at z = h. Both plates are stationary. The y direction is "into the paper. " Pressure is varying in the x direction from high on the left to lower on the right. The fluid is moving from left to right (i.e., in the x direction) with a velocity which depends on z, and with velocity v=0 at z = 0 and z = h.

Focus attention of the layer of fluid in the lower half of the channel, between z and $z + \Delta z$, and draw a free body diagram on the section of this layer situated between x and $x+\Delta x$. In this free body diagram, show the horizontal forces exerted on this fluid section from the layers above and below, and from behind and in-front.

I hope you will be willing to participate in this exercise.

Chet

 

[Chestermiller]

This is not a free body diagram. But it gets the point across:
View attachment 235820

As you can see, force is lessened at point 2.

The frictional force per unit wall area is the same at points 1 and 2.

 

[Chestermiller]

Not about momentum. But about the description of the two plates. Here is what you said:

"To get an idea of viscous friction, think extreme cases like very viscous fluids like molasses, pancake syrup, and corn syrup. Imagine that you have the fluid contained between two horizontal parallel plates, and you are trying to slide the top plate to the right at constant speed. You need to exert a force on the upper plate to the right and a force on the lower plate to the left to hold it in place. OK so far?"

This is how I interpreted it:
View attachment 235821

It seems you are wanting to oppose the fluid moving with the plates - so "holding it in place" as you said ("it" being the fluid) while you move the plates, the upper plate to the right and the lower plate to the left.

No. The lower plate is not moving.

 

[BvU]

is to imply that the force is acting at the center of the fluid [edit, BvU:] only

No, it is not implied. Wherer do you get that idea ?

 

[boneh3ad]

it applies to this problem, the force pushing the fluid against friction (pushing the fluid from left to right) is getting reduced.

Why do you think the force is getting reduced? Across a small fluid element, the net forforce due to pressure is bases on the pressure difference from one side to the other, not simply the pressure on one side. This, taken to it's infinitesimal limit, implies that force is proportional to thrthe press gradient, not thethe press itself. So, a constant force requires qnconstsnt pressure gradient, not a constant pressure.

 

[Chestermiller]

To say that momentum is transported sideways is to imply that the force is acting at the center of the fluid, and the radial fluid is carried along by shear stress (thus momentum). When I asked before if the force is acting on the middle, I was told no, it acts against the cross sectional area all at once.

Is this what you mean:

View attachment 235817

This is close to what I'm saying, except that there should be an arrow on the left for each of the shells.