How Does Total Internal Reflection Occur in Salt Solutions?

[Anton Alice]

Hello,

please take a look at the following picture:

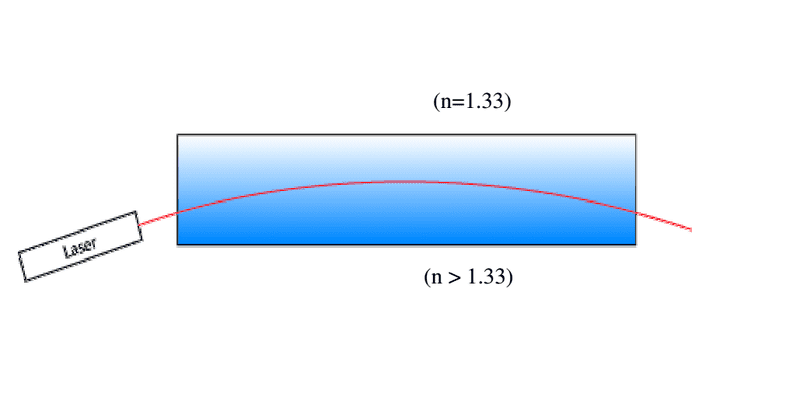
So we have a salt solution, with increasing refractive index, as you go down the solution.
The Laser is steadily refracted at the layers from high-to-low index and therefore bends in clockwise direction.
But how is it possible for the laser to bend down again? And also, shouldn't we also see reflections? Because at any point, there is a layer of high-to-low index transition. And at any such point there should also be a reflection. And as the angle of incidence get higher, as the laser path gets more horizontal, the reflection should dominate.

EDIT:

Does it bend down, because of total internal reflection at the peak of the curve?

 

[jfizzix]

Since the index of refraction changes continuously, you have to use Snell's law to describe the propagation one infinitesimal distance at a time. If you work it out, you can get a differential equation that will describe the trajectory of a beam of light. That it bends back downwards at the top is due to total internal reflection.

That being said, as the difference in index of refraction on two sides of an interface goes to zero, transmission dominates over reflection (the reflection coefficient becomes insignificant compared to the transmission coefficient). Though this would seem to contradict the idea of total internal reflection causing the backwards bend at the top, the beam near the top has a very shallow angle of incidence on either side of the peak, so that very small differences in refractive index can still amount to a change in the beam's trajectory.

 

[Anton Alice]

yes, thank you.