mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
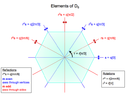
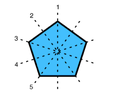
I want to find how many different necklaces we can create with $m$ symmetric beads if we have $k$ colours. Burnside's Formula is the following: $$\text{ # orbits } =\frac{1}{|G|}\sum_{g\in G} X (g)$$
In this case $G$ is the group of the permutations of the symmetric beads, or not? (Wondering)
And $X(g)$ is the number of elements that $g$ leaves unchanged, right? But how can we find this number in this case? Could you give me a hint? (Wondering)
I want to find how many different necklaces we can create with $m$ symmetric beads if we have $k$ colours. Burnside's Formula is the following: $$\text{ # orbits } =\frac{1}{|G|}\sum_{g\in G} X (g)$$
In this case $G$ is the group of the permutations of the symmetric beads, or not? (Wondering)
And $X(g)$ is the number of elements that $g$ leaves unchanged, right? But how can we find this number in this case? Could you give me a hint? (Wondering)