- #36
Baluncore
Science Advisor
2023 Award
- 15,660
- 9,399
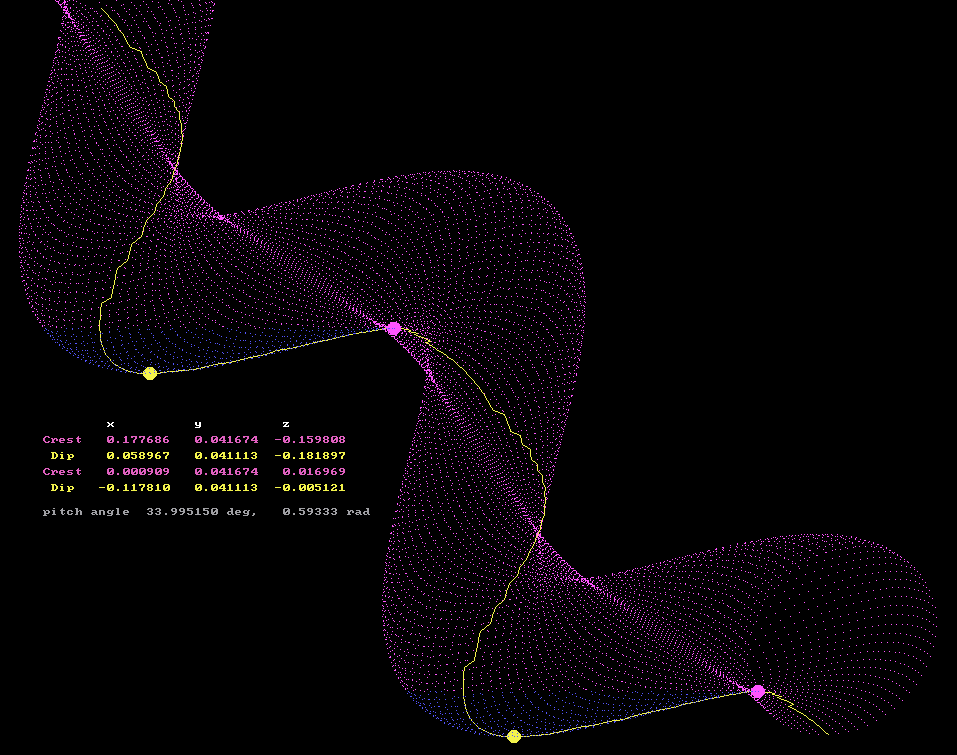
Here is a view of your helical tube.
X is to the right. Y is away from viewer. Z is up.
Helix axis passes through origin at angle of 45°.
Yellow line is valley. Yellow circle is where ball will rest in dip.
Magenta circle is a crest. Blue is volume that will hold a liquid.
X is to the right. Y is away from viewer. Z is up.
Helix axis passes through origin at angle of 45°.
Yellow line is valley. Yellow circle is where ball will rest in dip.
Magenta circle is a crest. Blue is volume that will hold a liquid.