How to determine angular velocity about a certain axis?

[vcsharp2003]

Homework Statement

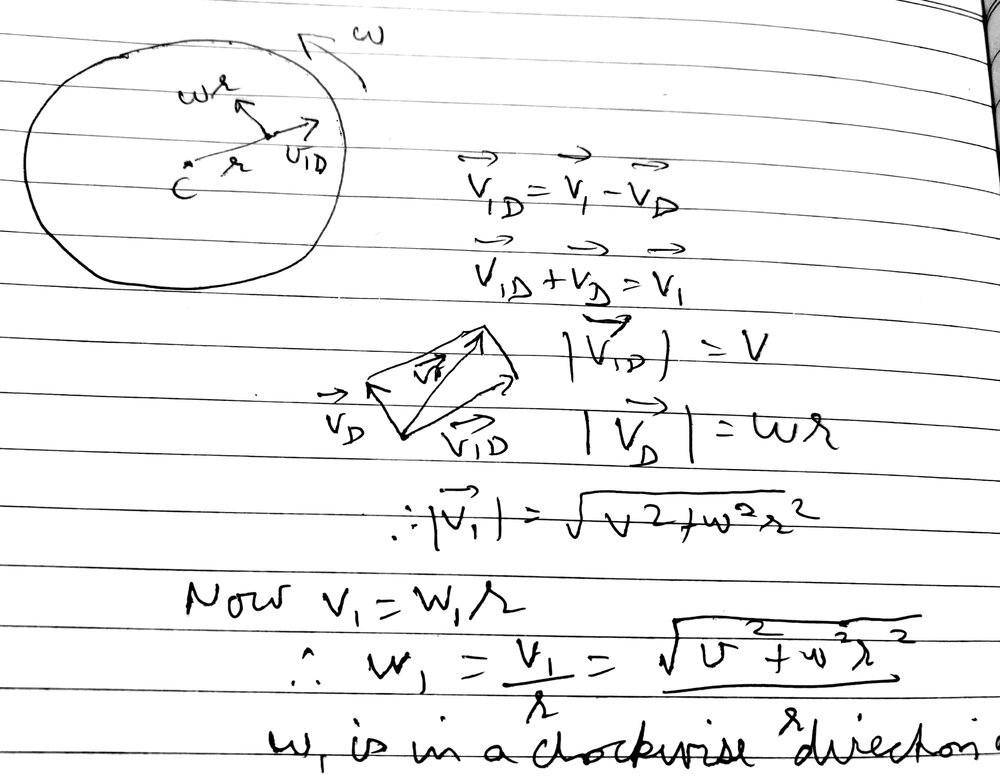
A disk is rotating counter clockwise at an angular speed of $\omega$ in a horizontal plane about its center. A small insect at its center starts to crawl outwards at a constant speed of $v$ relative to disk in a radial direction. What will be the angular velocity ( i.e. magnitude and direction) of the crawling insect at any instant?

Relevant Equations

v=wr

If the crawling insect were stationary at a certain instant of time, then it would have the same angular velocity as that of disk, which is w in a clockwise direction. But now it's velocity at any instant is the vector sum of velocity due to rotation and the velocity it crawls at. My attempt is as shown below.

 

[PeroK]

What's the definition of angular velocity? How it is represented in polar coordinates?

 

[vcsharp2003]

What's the definition of angular velocity?

The definition is as below.

Angular velocity = $\dfrac {d\theta} {dt}$

How it is represented in polar coordinates?

This part is not clear. I know the polar coordinates at any instant for insect will be $(r,\theta)$.

 

[PeroK]

The definition is as below.

Angular velocity = $\dfrac {d\theta} {dt}$

Isn't that your answer? That is using polar coordinates.

 

[vcsharp2003]

Isn't that your answer? That is using polar coordinates.

Yes, since $\theta$ is one of the polar coordinates.

 

[vcsharp2003]

Isn't that your answer? That is using polar coordinates.

It seems that the radius vector $\vec r$ is rotating at the angular velocity of the disk.
So the insect will also be having an angular velocity of w in a counter clockwise direction.
Is that the correct logic?

 

[PeroK]

It seems that the radius vector $\vec r$ is rotating at the angular velocity of the disk.
So the insect will also be having an angular velocity of w in a counter clockwise direction.
Is that the correct logic?

It must be.

 

[Steve4Physics]

It seems that the radius vector $\vec r$ is rotating at the angular velocity of the disk.
So the insect will also be having an angular velocity of w in a counter clockwise direction.
Is that the correct logic?

Can I chip-in? - as it sounds like you may not be entirely convinced/confident.

Imagine a radius drawn on the disc and the insect walks along this radius.

During any time-interval Δt, the angular displacements of the disc and insect must be identical - because they are both the same as the angular displacement of the radius, Δθ.

 

[vcsharp2003]

Imagine a radius drawn on the disc and the insect walks along this radius.

Yes, that makes it easier to understand since the drawn radius undergoes the same angular displacement as the disk. Very neat!

 

[vcsharp2003]

It must be.

I am trying an alternative approach as explained below. It seems correct to me.

In the formula, $v ={\omega} \, r$, can we say that $v$ must always be the tangential speed at a distance $r$ from center of a rotating point?

If yes, then using the relative velocity vector diagram shown in my attempted solution, it can be said that $V_{d}$ is the tangential component of $V_{i}$. Hence $V_{d} = {\omega}_{i} \, r$. It then follows that ${\omega}_{i} = \dfrac {V_{d}} {r}=\dfrac { {\omega} \, r} {r} = {\omega}$.

 

[vcsharp2003]

I am trying an alternative approach as explained below. It seems correct to me.

In the formula, $v ={\omega} \, r$, can we say that $v$ must always be the tangential speed at a distance $r$ from center of a rotating point?

If yes, then using the relative velocity vector diagram shown in my attempted solution, it can be said that $V_{d}$ is the tangential component of $V_{i}$. Hence $V_{d} = {\omega}_{i} \, r$. It then follows that ${\omega}_{i} = \dfrac {V_{d}} {r}=\dfrac { {\omega} \, r} {r} = {\omega}$.

The above fact of $v$ being tangential speed is absolutely correct according to some textbooks I consulted. Therefore, my approach as mentioned in post#10 is correct and an alternative approach to proving that angular velocity of insect at any instant is the same as angular velocity of disk.