arestes
- 84
- 4
- TL;DR Summary
- Power is assumed to be given (a constant) when justifying why we need high voltage to minimize losses through the lines. However, I think power depends on load.
Hello:
I'm confused about transmission lines. According to Faraday's Law, what's induced is an emf that depends on how fast the coils spin, or whatever equivalent to a simple model seen on Physics textbooks.
Power, however, is then assumed constant when talking about the power loss due to heating (##P_{loss}=I^2R ##I2R). Current is obtained from the power P generated at the station:
$$ IV=P_{gen} \rightarrow I=\frac{P_{gen}}{V}$$
Therefore:
$$ P_{loss} =\frac{P^2_{gen}}{V^2}R$$
My question is: According to a simple schematics of a transmission line (taken from wikipedia):
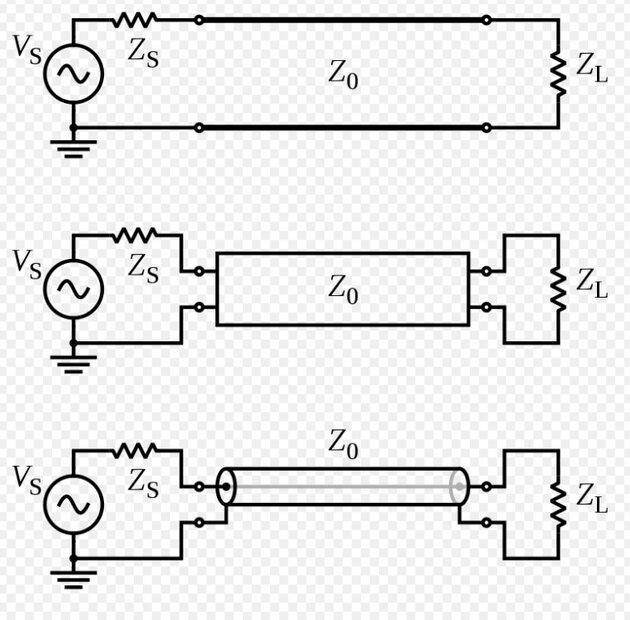
The impedance of the load is part of the circuit, it makes sense that if load changes (which is what users do) then power delivered is changed. Therefore, what we extract from the station depends upon the load, which makes sense.
But this contradicts the argument that we only need to maximize V on the denominator in the expression of ##P_{loss}##
In real life, how is this taken into account? Is the load impedance assumed constant? (I think there are conditions for maximum power delivery of impedance matching). Variations of impedance are negligible?
Thanks for any clarifications on this topic. By the way, I need this to have a crystal clear explanation of why we need to have high voltages in transmission lines from a Physics perspective but this seems to touch on electrical engineering matters.
V=P→I=PV
I'm confused about transmission lines. According to Faraday's Law, what's induced is an emf that depends on how fast the coils spin, or whatever equivalent to a simple model seen on Physics textbooks.
Power, however, is then assumed constant when talking about the power loss due to heating (##P_{loss}=I^2R ##I2R). Current is obtained from the power P generated at the station:
$$ IV=P_{gen} \rightarrow I=\frac{P_{gen}}{V}$$
Therefore:
$$ P_{loss} =\frac{P^2_{gen}}{V^2}R$$
My question is: According to a simple schematics of a transmission line (taken from wikipedia):
The impedance of the load is part of the circuit, it makes sense that if load changes (which is what users do) then power delivered is changed. Therefore, what we extract from the station depends upon the load, which makes sense.
But this contradicts the argument that we only need to maximize V on the denominator in the expression of ##P_{loss}##
In real life, how is this taken into account? Is the load impedance assumed constant? (I think there are conditions for maximum power delivery of impedance matching). Variations of impedance are negligible?
Thanks for any clarifications on this topic. By the way, I need this to have a crystal clear explanation of why we need to have high voltages in transmission lines from a Physics perspective but this seems to touch on electrical engineering matters.
V=P→I=PV