Hydrostatic pressure and the reading on a scale

[refracted]

http://www.thenakedscientists.com/HTML/content/kitchenscience/exp/weighing-buoyancy/So I was wondering if both the scales would show the same weight value? (the scales are marked black in the picture)

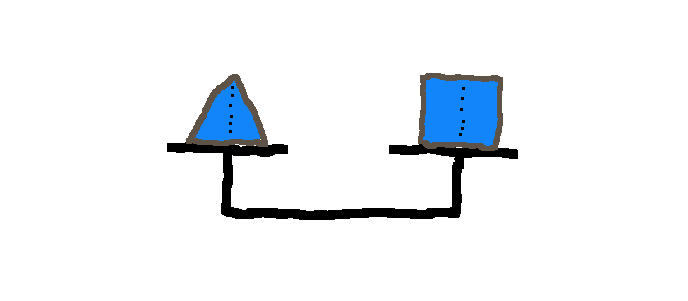
The object on the left is a pyramid and the object on the right is a cube.
They are both filled with water.
We assume the masses of the containers are the same.

My question is, if the height h is the same, and the bottom area of both the objects is the same, would they "weigh" the same amount on the scale? (regardless of the cube having three times the volume of the pyramid)

Since hydrostatic pressure is p = ρgh and force F = pA, the volume of the water shouldn't matter.

It does sound very absurd, however.
So my question is, is the last statement of this article wrong?
http://www.thenakedscientists.com/HTML/content/kitchenscience/exp/weighing-buoyancy/

Or does the amount of hydrostatic pressure really affect the shown weight of the water in total?

Thanks! :)

(click the picture to zoom)

 

[russ_watters]

Welcome to PF!

The forces internal to the pyramid are not the same as the force the pyramid applies to the scale. Consider that if you attach a string to the top of the pyramid, you could lift it.

 

[refracted]

Yeah that's what I thought. As it did sound very absurd to me.
I guess the final part of that article was wrong, after all.

Thanks!

 

[jbriggs444]

Yeah that's what I thought. As it did sound very absurd to me.
I guess the final part of that article was wrong, after all.

The final part of the referenced article was:

"Another way of thinking of it is that when you put your finger in the water, it will increase the level of water in the cup. This means that there is more water pressure at the bottom of the cup, acting on the same area, so there is a greater force."

That is not incorrect. It is a simplification that implicitly assumes a cylindrical cup. In a cylindrical cup you can ignore the effect of water pressure on the cup sides.

With a pyramidal cup, water pressure on the sides matters. But that does nothing to alter the fact that putting your finger into a pyramidal cup of water results in a net downward force on the water equal to the weight of water displaced by your finger.

It does mean that the down-force of water on a pyramidal cup is accurately calculated based on volume and is not accurately calculated based on height times area at the bottom.

 

[refracted]

But doesn't the increased total weight of the system essentially come from the counter-upthrust when you put your finger in the cup?
(so that total weight = G + counter upthrust)

Putting your finger in the cup does increase the hydrostatic pressure of the water,
but shouldn't it only increase the pressure on the sides of the container
and not cause the system to actually weigh more? (like russ_watters said)

Because that's what I think they meant in the final part of the article, and I can't get how that could be true.

Thanks for contributing!

 

[A.T.]

But doesn't the increased total weight of the system essentially come from the counter-upthrust when you put your finger in the cup?
(so that total weight = G + counter upthrust)

Yes, that's why they call it "weighing buoyancy".

Putting your finger in the cup does increase the hydrostatic pressure of the water,
but shouldn't it only increase the pressure on the sides of the container

That is not possible. At every point the pressure is the same in all directions.

 

[jbriggs444]

But doesn't the increased total weight of the system essentially come from the counter-upthrust when you put your finger in the cup?
(so that total weight = G + counter-upthrust)

There is often more than one way to explain the same effect.

If the explanation that resonates with you is Newton's third law and the fact that the buoyancy of the water on your finger must be equal and opposite to the "counter-upthrust" of your finger pushing down on the water then that is fine.

That does not mean that other ways of accounting for the increase in the total downforce of the cup on the scale are automatically incorrect.

Putting your finger in the cup does increase the hydrostatic pressure of the water,
but shouldn't it only increase the pressure on the sides of the container
and not cause the system to actually weigh more? (like russ_watters said).

Pressure in a fluid is not directional. If pressure increases on the sides then pressure also increases on the bottom.

The experimental apparatus in the article with which you are disagreeing is a balance scale. The question isn't which side of the system "actually weighs more". The question is which side of the balance sinks toward the floor.

If the cup is cylindrical then the downforce of water on cup is equal to the pressure on the bottom of the cup multiplied by the area of the bottom of the cup.

Because that's what I think they meant in the final part of the article, and I can't get how that could be true.

What do you take the final part of that article to be saying that you disagree with?

 

[refracted]

There is often more than one way to explain the same effect.

If the explanation that resonates with you is Newton's third law and the fact that the buoyancy of the water on your finger must be equal and opposite to the "counter-upthrust" of your finger pushing down on the water then that is fine.

That does not mean that other ways of accounting for the increase in the total downforce of the cup on the scale are automatically incorrect.

Yes, there was no problem for me to understand that. :)

I didn't mean to put it that way, though, I just couldn't get the thing about hydrostatic pressure into my head.

The experimental apparatus in the article with which you are disagreeing is a balance scale. The question isn't which side of the system "actually weighs more". The question is which side of the balance sinks toward the floor.

If the cup is cylindrical then the downforce of water on cup is equal to the pressure on the bottom of the cup multiplied by the area of the bottom of the cup.

So, hydrostatic pressure depends solely on the height of the water column, but the actual "hydrostatic force" (downforce of the water column) depends on how much water there is actually on top of the bottom surface. (for a cylinder, all the water at the surface is on the same line with the bottom surface.)

So as for a pyramid, the downforce isn't the same as for a cube of the same bottom area, because on the pyramid, there's is only one line where the whole height of the water column transfers to the bottom.

If that's correct, it makes much more sense now. Thank you for your explanation! :)

Do you happen to know where I could read more about hydrostatic pressure concerning this issue, specifically?

 

[256bits]

So, hydrostatic pressure depends solely on the height of the water column, but the actual "hydrostatic force" (downforce of the water column) depends on how much water there is actually on top of the bottom surface. (for a cylinder, all the water at the surface is on the same line with the bottom surface.)

So as for a pyramid, the downforce isn't the same as for a cube of the same bottom area, because on the pyramid, there's is only one line where the whole height of the water column transfers to the bottom.

I am not sure what you ae getting at. The force on the bottom internal surface of both the cube and the pyramid are the same. You already state that in your first post:

Since hydrostatic pressure is p = ρgh and force F = pA, the volume of the water shouldn't matter.

Rather than using a pyramid for the left container, for ease of expalnation, use one half of a cube cut along a diagonal so it is then a traingular shaped solid. There will now be one half as much water in the left container as in the cube, but since the height of the water is the same in both, the equations p = ρgh and force F = pA still apply. Both bottom surfaces have to be of the same strength to contain the pressure ( being the same in both instances )

So why do they not weigh the same if the statement at the end of the article is correct - ie both have the same pressure and thus force from the water on the bottom surface of each container?

To see why, reflect back on the picture you drew, which has both containers resting on a surface of the balance. The pressure of the containers on this surface is what counts for the balance and you have to agree that the left triangular has one half as much pressure on this surface as the cube does. Half as much pressure on the same surface area means that the left container weighs half as much as the cube on the right.

Internal forces:
Do not matter but you can calculate them anyways to see why.
For the internal bottom surfaces of both containers, the pressure and force is just p = ρgh and force F = pA.
Since the right container, a cube has straight vertical faces, that is the only vertical force.

The left container, the triangular one, though has a slanted surface so there must be both a vertical and horizontal force on it due to the pressure of the water. It so happens that the force is the average of the force due to pressure at the top of the slant and the force due to pressure at the bottom of the slant. That turns out to be F/2.
The left container then has an F pushing down on the flat bottom surface, and an F/2 pushing up on the slanted surface, for a total of F/2 acting on the whole container.
Which, by the way, is what we expect - that the left container weighs half as much as the right container.

It is much easier to just do an W = mg, to calculate the weight, and forget about all the internal forces in a lot of situations.

You were already answered in the other posts, but perhaps this puts some perspective on it.

you might find this interesting.
http://www.sfu.ca/~ptaherib/teaching/ENSC_283/Course%20notes/Hydrostatic%20Force%20on%20a%20Submerged%20Surface.pdf

 

[refracted]

I am not sure what you ae getting at. The force on the bottom internal surface of both the cube and the pyramid are the same. You already state that in your first post:


Rather than using a pyramid for the left container, for ease of expalnation, use one half of a cube cut along a diagonal so it is then a traingular shaped solid. There will now be one half as much water in the left container as in the cube, but since the height of the water is the same in both, the equations p = ρgh and force F = pA still apply. Both bottom surfaces have to be of the same strength to contain the pressure ( being the same in both instances )

So why do they not weigh the same if the statement at the end of the article is correct - ie both have the same pressure and thus force from the water on the bottom surface of each container?

To see why, reflect back on the picture you drew, which has both containers resting on a surface of the balance. The pressure of the containers on this surface is what counts for the balance and you have to agree that the left triangular has one half as much pressure on this surface as the cube does. Half as much pressure on the same surface area means that the left container weighs half as much as the cube on the right.

Internal forces:
Do not matter but you can calculate them anyways to see why.
For the internal bottom surfaces of both containers, the pressure and force is just p = ρgh and force F = pA.
Since the right container, a cube has straight vertical faces, that is the only vertical force.

The left container, the triangular one, though has a slanted surface so there must be both a vertical and horizontal force on it due to the pressure of the water. It so happens that the force is the average of the force due to pressure at the top of the slant and the force due to pressure at the bottom of the slant. That turns out to be F/2.
The left container then has an F pushing down on the flat bottom surface, and an F/2 pushing up on the slanted surface, for a total of F/2 acting on the whole container.
Which, by the way, is what we expect - that the left container weighs half as much as the right container.

It is much easier to just do an W = mg, to calculate the weight, and forget about all the internal forces in a lot of situations.

You were already answered in the other posts, but perhaps this puts some perspective on it.

you might find this interesting.
http://www.sfu.ca/~ptaherib/teaching/ENSC_283/Course%20notes/Hydrostatic%20Force%20on%20a%20Submerged%20Surface.pdf

Thanks a lot for the in-depth reply and the link.
I still have a question. Would the case be exactly the same if we were using two different scales to weigh the object instead of using one single balance scale?

 

[A.T.]

Would the case be exactly the same if we were using two different scales to weigh the object instead of using one single balance scale?

You will measure a weight increase with a spring scale too. And now to test what you have learned try these questions:

1) You have a balance scale with two identical metal spheres, hanging on it. Then a two pan balance scale with a bucket on each pan. One bucket contains water, the other one ethanol. Initially both scales are perfectly balanced. What happens with the scales if you lower the metal spheres into the buckets (each sphere in one of the buckets), so they are submerged completely?

2) Does the load on the pillars of a water bridge (see here) increase, when a ship passes over the bridge?

 

[refracted]

You will measure a weight increase with a spring scale too. And now to test what you have learned try these questions:

1) You have a balance scale with two identical metal spheres, hanging on it. Then a two pan balance scale with a bucket on each pan. One bucket contains water, the other one ethanol. Initially both scales are perfectly balanced. What happens with the scales if you lower the metal spheres into the buckets (each sphere in one of the buckets), so they are submerged completely?

2) Does the load on the pillars of a water bridge (see here) increase, when a ship passes over the bridge?

Thanks for the clarification.

1. The scale would turn down towards the bucket of water. Because water is denser than ethanol, the extra density adds to the hydrostatic pressure increase or counter upthrust caused by the spheres when they displace the same amount of liquid.

2. Yes. To make the ship float in the first place, the water needs to support it with buoyancy or upthrust. However, the ship applies an equal and opposite force on the water, which not only presses the water down, but therefore caused more force applied to the bridge itself.
You could measure it by calculating the hydrostatic pressure increase when the ship raises the surface of the water by making room for itself. However, this is a bit more complicated to calculate, because the increased water surface starts to make itself even along the whole length of the bridge due to pressure differences.

I think the major problem for me in the first place was to understand that the force caused by hydrostatic pressure is affected by the shape of the object. I've always been taught that hydrostatic pressure depends solely on the height and the density of the liquid (and g, of course), which is true, but the case isn't necessarily the same for the force caused by hydrostatic pressure, which requires the shape of the object to be taken into account.

 

[A.T.]

1. The scale would turn down towards the bucket of water. Because water is denser than ethanol, the extra density adds to the hydrostatic pressure increase or counter upthrust caused by the spheres when they displace the same amount of liquid.

Correct, and what about the other scale, on which the two spheres are hanging?

2. Yes. To make the ship float in the first place,

But the ship is already floating, when it is 10km away from the bridge. The question is, if the load on the pillars increases, as the ship goes onto the bridge. It is not a question about dynamic effects like waves. Let's say the ship stops on the bridge for a while. Is the load on the pillars higher, compared to when the ship was 10km away?

 

[refracted]

Correct, and what about the other scale, on which the two spheres are hanging?


But the ship is already floating, when it is 10km away from the bridge. The question is, if the load on the pillars increases, as the ship goes onto the bridge. It is not a question about dynamic effects like waves. Let's say the ship stops on the bridge for a while. Is the load in the pillars higher, compared to when the ship was 10km away?

1. The sphere which was submerged in the water would cause the scale to turn towards the other sphere which was submerged in ethanol. This is because the water-submerged sphere feels a greater buoyancy.

2. I was just describing why the ship floats in general. :)
Please check the rest of that answer to see if it's any good. :)

Thanks!

 

[A.T.]

Please check the rest of that answer to see if it's any good. :)

Well...

because the increased water surface starts to make itself even along the whole length of the bridge

Why only the length of the bridge, and not the length of the canal? The question is: After the ship already floats somewhere in the canal, does the water level on the bridge rise, when the ship moves onto the bridge? (Slow moving / drifting with the water, no waves etc.)

 

[refracted]

Well...

Why only the length of the bridge, and not the length of the canal? The question is: After the ship already floats somewhere in the canal, does the water level on the bridge rise, when the ship moves onto the bridge? (Slow moving / drifting with the water, no waves etc.)

Could it be then that the reaction for buoyancy also distributes evenly along the water of the bridge and the canal, meaning the bridge actually faces little to no additional load?

The thing is that while the buoyancy is still there (to keep the ship floating), the additional force, that the ship causes due to the increase in hydrostatic pressure (water column height) or the reaction of buoyancy, distributes so evenly along the canal and the bridge that it's hard to notice.

Additional question: Is it still true, though, that the bridge has to be strong enough to support the weight of the water itself on top of it? (the weight of the prism-like shape of water from the end of the bridge to the other end)
Meaning that if you suddenly put two big water blocks on both ends of the bridge, the load on the bridge would stay the same? (We assume the blocks are put in a way so that the amount of water on top of the bridge remains the same)

 

[A.T.]

Could it be then that the reaction for buoyancy also distributes evenly along the water of the bridge and the canal, meaning the bridge actually faces little to no additional load?

Right. But that additional load is already added when you put the ship into the water, somewhere in the canal. After that, moving the ship over the bridge doesn't increase the load anymore.

Additional question: Is it still true, though, that the bridge has to be strong enough to support the weight of the water itself on top of it?

Yes.

 

[refracted]

Right. But that additional load is already added when you put the ship into the water, somewhere in the canal. After that, moving the ship over the bridge doesn't increase the load anymore.


Yes.

Thanks for the accurate explanation! I think I got this now. :)