Hydrostatic pressure inside an inverted tube

[lost captain]

TL;DR Summary

What's the total pressure ( Patm and Phydrostatic) inside an inverted tube? I am basically referring to that straw experiment we do in physics class when the teacher explains atmospheric pressure.

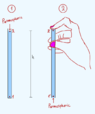
When we learn about atmospheric pressure in physics class, there's this classic experiment with a straw (second drawing). So i wanted to ask about the hydrostatic pressure in that particular experiment.

Is the total pressure at point 1' equal to Patm + ρgh ? So is the total pressure at point 1' essentially the same as the total pressure at pont 1 in the first container? And what about points 2 and 2' do they also have the same pressure?

And just to clarify one more very important thing: when a container filled with water is open to the atmosphere, is the atmospheric pressure distributed throughout the whole container? So, does any point, at any depth, in that container have the same atmospheric pressure?

 

[Baluncore]

Welcome to PF.
Start at the point where the pressure is known to be atmospheric. Points 2 and 1'.

If you go down a water column from there, the absolute pressure increases due to hydrostatic pressure. The pressure at your point 1, is greater than atmospheric.

If you go up a water column from atmospheric, the absolute pressure reduces.
The pressure at your point 2', is less than atmospheric.

 

[lost captain]

Thank you for taking the time to reply to my question, I've been struggling with this for a week.
At point 1' there is the atmospheric pressure( point 1' is open to the atmosphere) but also there is hydrostatic pressure due to the weight of all the water above point 1'. So why do we say the pressure at point 1' is only the atmospheric pressure?

 

[Baluncore]

So why do we say the pressure at point 1' is only the atmospheric pressure?

1. Because if it was greater than atmospheric pressure, the water would flow out of the tube.
2. The water is pushed up by atmospheric pressure only, the pressure at the top, 2', against the plug, is less than atmospheric pressure by the hydrostatic pressure of the column.
3. If the straw was very long, it would be a water barometer, closed at the top, so there would be a vacuum above the water column. The hydrostatic pressure, as you go upwards, must therefore reduce.

Note: that with water, the top of a barometer tube is filled with water vapour, not vacuum.

 

[lost captain]

1. Because if it was greater than atmospheric pressure, the water would flow out of the tube.
2. The water is pushed up by atmospheric pressure only, the pressure at the top, 2', against the plug, is less than atmospheric pressure by the hydrostatic pressure of the column.
3. If the straw was very long, it would be a water barometer, closed at the top, so there would be a vacuum above the water column. The hydrostatic pressure, as you go upwards, must therefore reduce.

Note: that with water, the top of a barometer tube is filled with water vapour, not vacuum.

Yes i can understand that, it does makes sense. But its not what we learned on class. We learned that a column of any liquid due to its weight creates hydrostatic pressure. Doesn't the weight of the water create hydrostatic pressure here?

Can't the point 1' have hydrostatic pressure from above and atmospheric pressure from below? I know we defined pressure, at a point, to be the same in all directionsthat but...i don't know
Does point 1' have hydrostatic pressure and if not why?

 

[Baluncore]

Does point 1' have hydrostatic pressure and if not why?

Atmospheric pressure at 1', is pushing the water column up the straw, against the plug at the top.

The pressure at 1' must be atmospheric. That comes from the weight of the water column, plus the "less than atmospheric pressure" against the plug at the top of the column.

The difference in pressure between 1' and 2' is the hydrostatic pressure of the column.

 

[lost captain]

So if i understand this right,
P1'= Phydrostatic at 1' (which is ρgh) + P -less than atmospheric- at 2'

Both Phydrostatic and P-less than atmospheric- are created due to the weight of the water
Right?

 

[Baluncore]

Both Phydrostatic and P-less than atmospheric- are created due to the weight of the water
Right?

Except, they are both referenced to the atmospheric pressure.
The difference in pressure between 1' and 2' is purely hydrostatic.
P_1' = atmospheric.
P_2' = P_1' - P_hydrostatic.

 

[lost captain]

Okay i think i finally understand this. Could you also confirm if im right in this example(picture below)? Now instead of a straw we have barometers of different heights filled with mercury. Are my statements in the picture correct?

 

[Baluncore]

That looks OK.
In that system, P2 is the unknown.

If there was a 10-metre-high glass-column water-barometer in a swimming pool, you could duck down into it, then begin to swim up the column. As you rise, the water has the same density, and swimming is the same, but the pressure is reducing so you must breathe out as you rise.

When you get to the surface inside, you find cold steam, without oxygen, your mouth and eyes prickle and bubble, then you begin to suffer from the bends as nitrogen comes out of solution in your blood. P2 is not a nice place to be.

 

[lost captain]

Thanks so much, really i couldn't have figured this out by myself, thank you

"As you rise, the water has the same density, and swimming is the same, but the pressure is reducing so you must breathe out as you rise."
And buoyancy is the same too right?

 

[Lnewqban]

... We learned that a column of any liquid due to its weight creates hydrostatic pressure. Doesn't the weight of the water create hydrostatic pressure here?

It is only the weight of the column of water what makes the pressure vary with the height.
Think of it as a metal bar that you are holding in place in the middle of the air in two ways:
1) Supported vertically on the palm of your hand.
2) Hanging vertically from the tip of your fingers.

The supported weight is the same, but the bar in #1 is pushing on your hand (most general case taught in class, atmospheric pressure at top and calculated pressure at bottom of the column), while in #2 the bar is pulling from your fingers (case of this problem, reverse of #1).

 

[A.T.]

Yes i can understand that, it does makes sense. But its not what we learned on class. We learned that a column of any liquid due to its weight creates hydrostatic pressure. Doesn't the weight of the water create hydrostatic pressure here?

Maybe the conceptual misunderstanding comes from the word "creates". It's better to say that a static column of liquid under gravity must have a pressure gradient to be in equilibrium, without getting into causation.

Can't the point 1' have hydrostatic pressure from above and atmospheric pressure from below?

Those pressures "from both sides" must be equal for equilibrium, but they don't "add up". Similarly, when you pull on a rope with a force F on each end, the tension in the rope is F, not 2F.